Vectors (Physics)
Posted by Sajid Khan | Last updated on
This page is split into multiple parts.
- Vectors (Physics) | Part-1
- Vectors (Physics) | Part-2
What is a Vector quantity?
A vector quantity is a quantity that has a magnitude as well as a direction.
The easiest example of a vector quantity is Force. If you apply force on a body, That force will always have a magnitude (The amount of force you’re putting on the body), as well as the direction (The direction in which you’re applying force on the body).
If a quantity is defined ONLY by its magnitude, that quantity is called a scalar quantity. Time, Volume, Mass are some examples of scalar quantities, they do have magnitude ( example: 5 seconds, 5 liters, 5 kg ), but they don’t have a direction.
Notation
A vector is generally written as a letter with an arrow above it (example: \( \vec{A} \)) or as a Bold letter.
Plane letters are used to denote only the magnitude of the Vector. Magnitude of vector is also denoted with the help of vertical bars on either side of the vector (example: \(\left| \vec A \right|\)).
To sum it up,
- Any vector named “A” can be written as: \(\vec A\) or \( \textbf{A} \)
- And it’s magnitude is written as: \(A\) or \(\left|\vec A\right|\) or \(\left| \textbf{A} \right|\)
- Throughout this tutorial, we might also use terms like “vector A” to denote \(\vec A\) or \(\textbf{A}\)
Graphical representation of vectors
Graphically, Vectors are represented by a line with an arrowhead at one end. The direction in which the arrowhead points represents the direction of the vector, and the length of the line represents its magnitude.

Symbol \(\hat a\) in the diagram above is a unit vector, Unit vectors are generally used to indicate the direction of any vector. We will talk more about it in the next section.
So, If you were applying a force of 10 newtons on a body to push it from left to right, then that force can be represented graphically as:
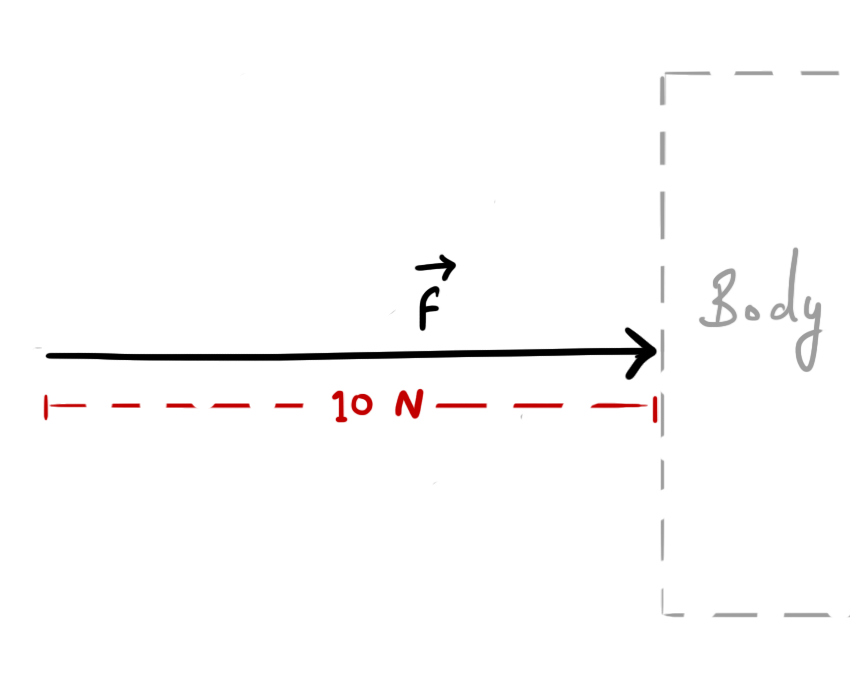
Unit Vectors
Any vector whose magnitude is unity ( equal to 1 ) is called a Unit Vector. A unit vector is denoted by a small letter with a hat symbol above it (example: \( \hat{a} \)).
Unit vectors are mostly used to indicate the direction of any vector. Unit vectors are also known as Direction vectors.
If a vector \(\vec V \) has magnitude V, and direction parallel to a unit vector \( \hat{v} \), then the vector \(\vec V \) can be written as the product of it’s magnitude and unit vector along it’s direction.
hence, \( \vec{V}=V\ \hat{v} \)
or \[ \hat{v}=\frac{\vec{V}}{V} \]
Note: Unit vectors having direction parallel to X, Y, or Z axis are usually written as \( \hat{i},\hat{j,}\text{ or }\hat{k} \) respectively (Or sometimes, written simply as \( i,j,\text{ or }k \)).
Parallel shifting of vectors
Remember, a vector quantity tells us about only it’s magnitude and direction. It doesn’t tell us anything about the position. This means that a vector doesn’t have a position.
So any vector can be drawn anywhere on the graph, regardless of its position.
Or, If we parallel shift a vector from one position to another on the graph without changing its direction and magnitude, the vector remains unchanged!
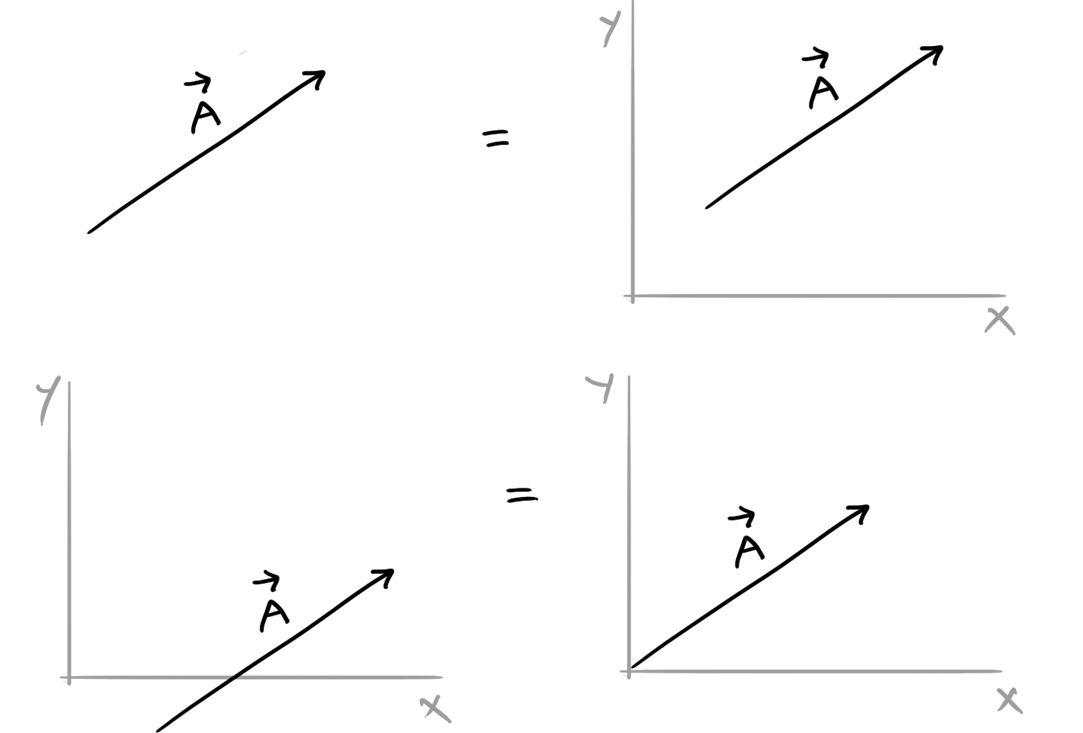
For simplicity, It is always a good idea to shift the tail of the vector to the origin.
Components of vector
As we already know that a vector \(\vec A\) whose magnitude is A and direction \(\hat a\), holds the relation \( \vec{A}=A\hat{a} \)
But, we still don’t know what direction is the direction of \(\hat a \)? It could be anything, left to right, top to bottom, or any other direction that we could draw on a paper. That is why, most of the time, vectors are represented with the help of some reference axes.
To represent a vector with the help of some reference axes, Any vector \(\vec A\) can be broken down to its multiple component vectors. Each component vector has a direction parallel to one of the reference axis (X, Y, or Z).
- When all the component vectors (of vector \(\vec A\)) add up together, they result in a single vector \(\vec A\).
- Addition of vectors or resultants is covered in upcoming sections. After reading vector additions, everything about “components of vector” will start to make sense (if it hasn’t already).
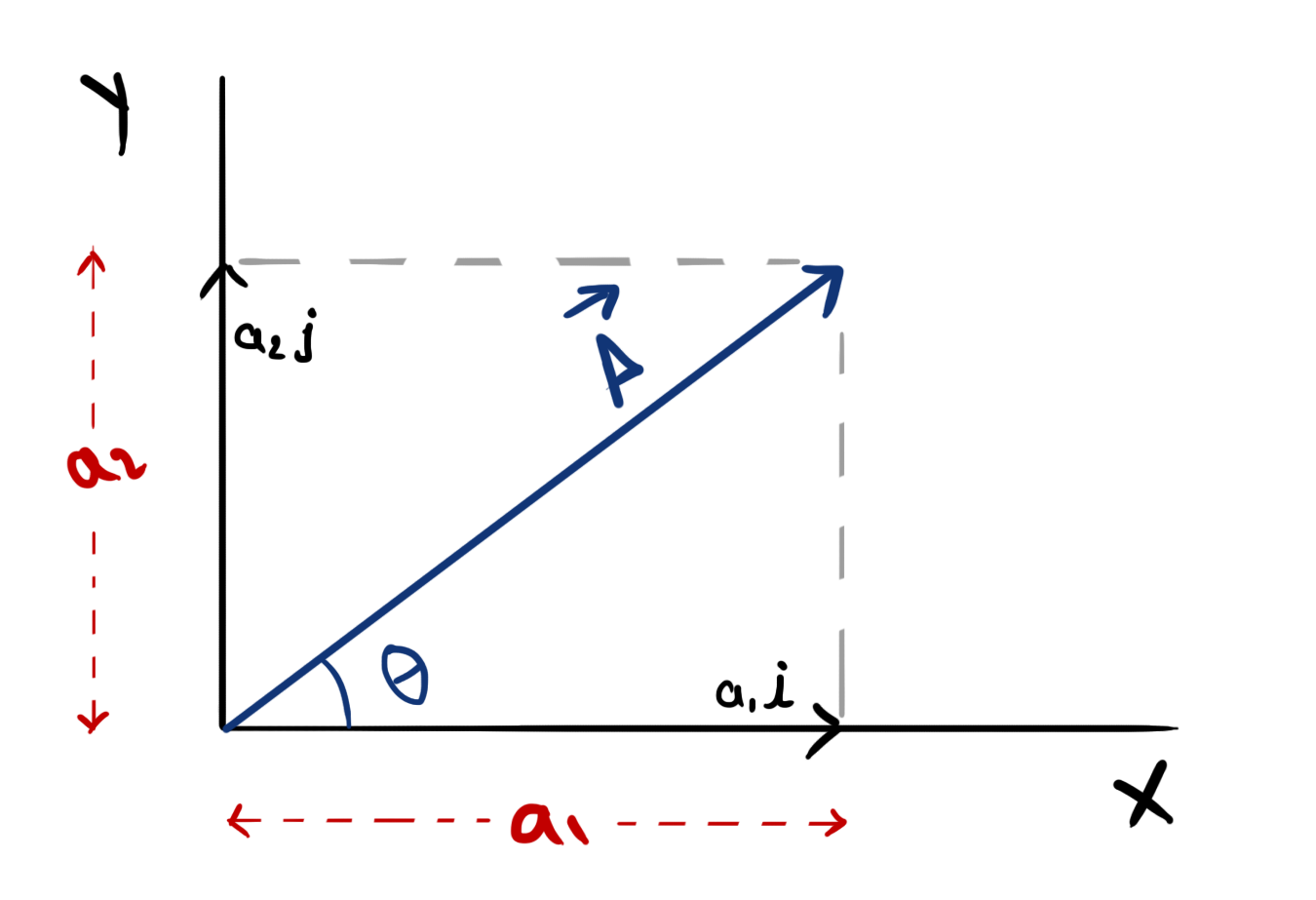
So the vector \(\vec A\) shown in the figure can be written as:
\( \vec{A}=a_1i+a_2j\) (sum of its component vectors)
- Here \(a_1i\) and \(a_2j\) are the component vectors of \(\vec A\) along X and Y axes.
- Just like any normal vector, Component vectors \(a_1i\) and \(a_2j\) has magnitude \(a_1\) and \(a_2\) with the direction along unit vectors i and j respectively.
- The direction of unit vectors i and j is known, it is along X and Y axis respectively.
Note: Only the magnitude part of the “component vector” of a vector is usually called just the “component” of vector.
For example, If vector \( \vec{A}=a_1i+a_2j \)
then, \( a_1i\text{ and }a_2j \) are the component vectors of \(\vec A\)
and, \( a_1\text{ and }a_2 \) are the components of \(\vec A\)
Magnitude of component vectors
For a vector \( \vec A=a_1i+a_2j \) as shown in figure above, With the help of trigonometric functions, it is clear that
\( a_1=A\cos\theta \), and
\( a_2=A\sin\theta \)
Here \(\theta\) is the angle made by the vector with horizontal axis, and A is the magnitude of vector \(\vec A\).
Magnitude of vector
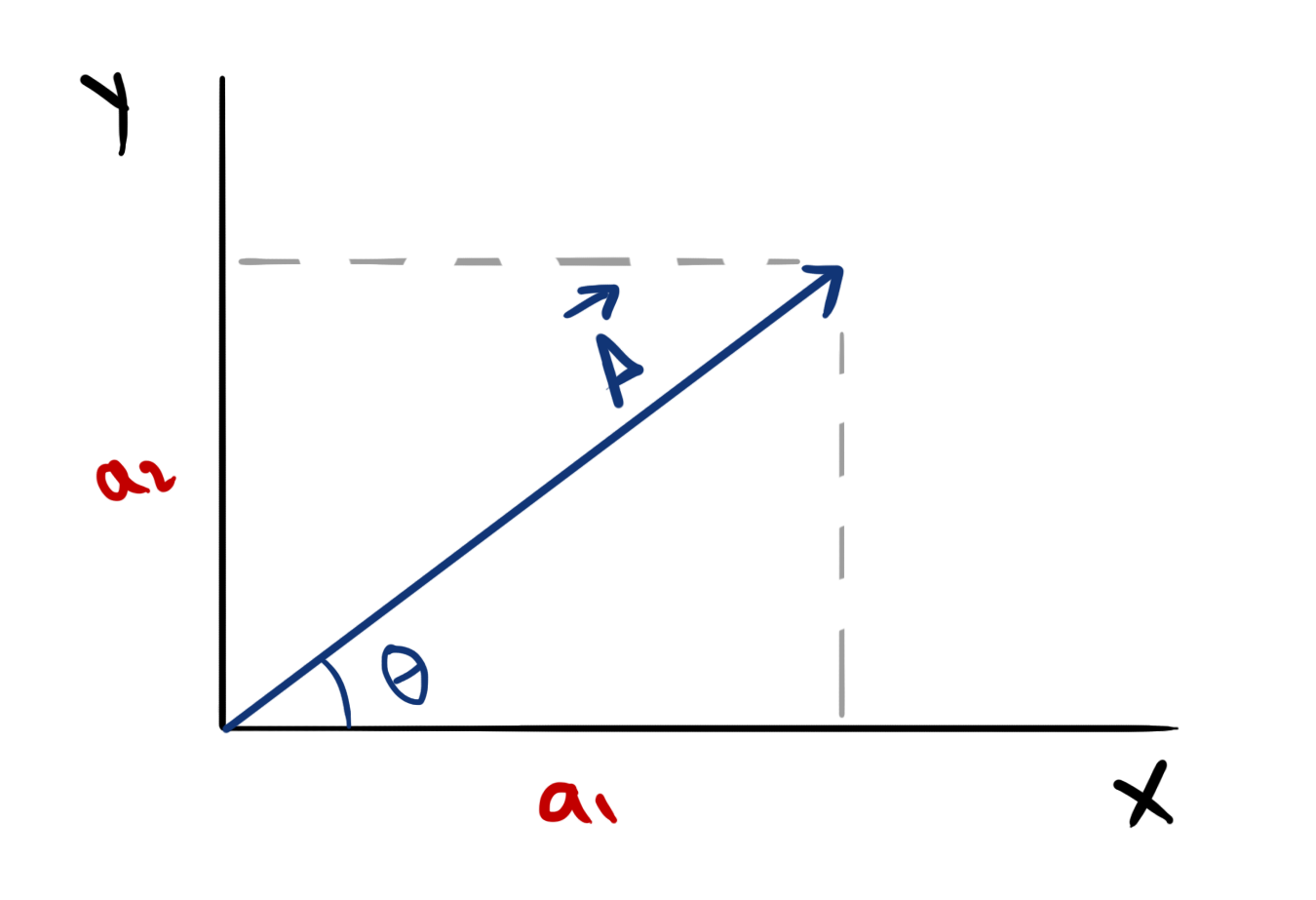
For a vector \( \vec A=a_1i+a_2j \) as shown in figure, With the help of Pythagorean theorem, it is clear that,
Magnitude \[ A=\sqrt{a_1^2+a_2^2} \]
Resultant vector
Resultant vector is the vector resulting from addition (or subtraction) of two or more vectors.
Addition of vectors
Addition of two vectors is easy!
If we had two vectors \( \vec{A}\text{ and }\vec{B} \), such that
\( \vec{A}=A\hat{a} \)
\( \vec{B}=B\hat{b} \)
Then, \( \vec{A}+\vec{B}=A\hat{a}+B\hat{b} \)
(At this point, you already know what \( A, B\text{ and }\hat{a}, \hat{b} \) are)
But again, What will be the direction and magnitude of the resultant vector \(A\hat{a}+B\hat{b}\)?
As usual, to know the direction and magnitude of the resultant vector, Component vectors of vector A and B are required. And there are other methods too for the vector addition, but before we jump to that, let’s first understand how the addition of vectors works in real life with the help of an example.
Example of vector addition
Consider a body placed on the ground (XY plane)
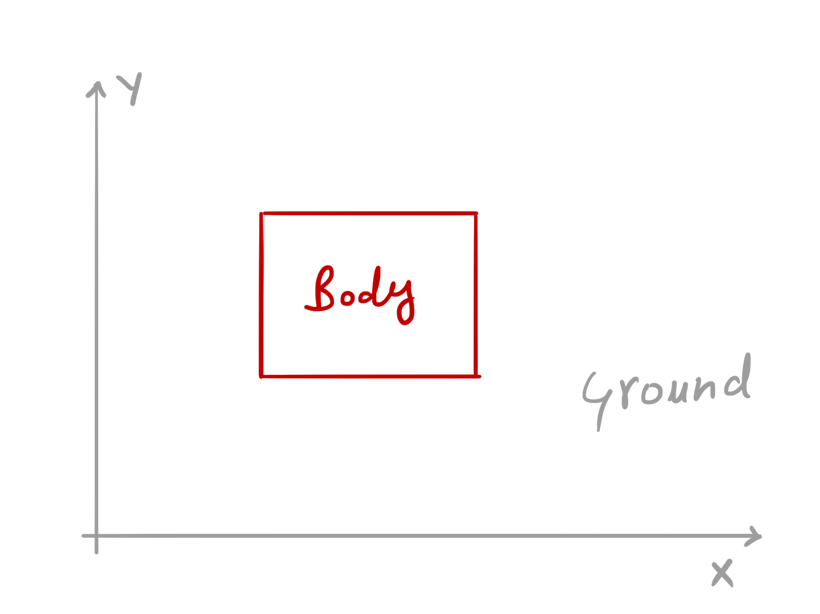
Let’s now apply a pulling force \( \vec{F_x} \) of magnitude Fx along the direction of X-axis. The body now will start moving in the direction of this force (in the direction of the X-axis).
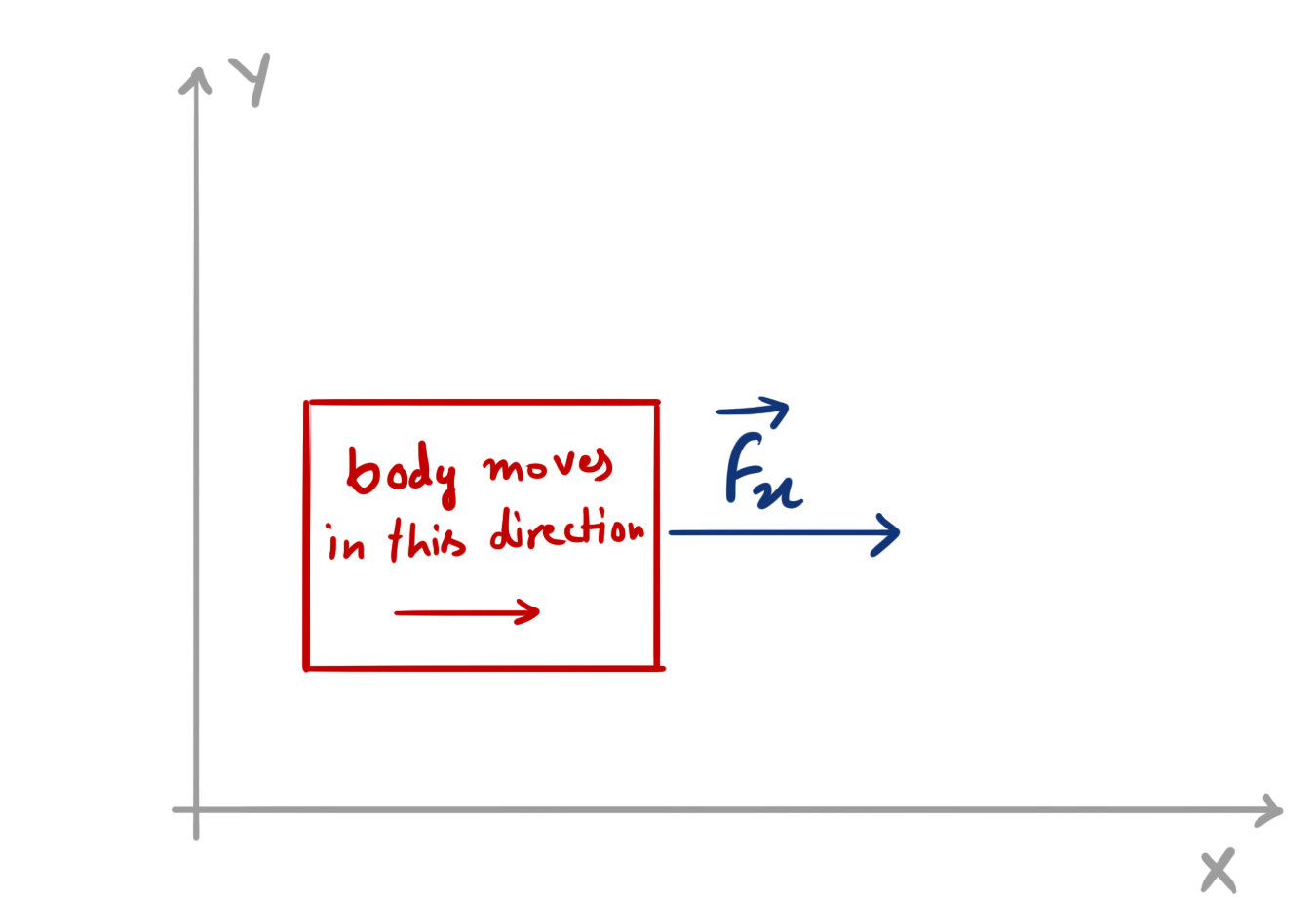
Or, similarly, If we apply a force \( \vec{F_y} \) of magnitude Fy along the direction of Y axis, The body will move in the direction of Y axis.
Note that the motion of body depends both on direction of force (direction of motion depends on it) as well as on the magnitude of the force (the amount of acceleration depends on it).
But, what if we apply both the forces \( \vec{F_x} \) and \( \vec{F_y} \) on the body at the same time? Obviously, the body won’t move in “only X” or “only Y” direction, It will move in a direction which is a combination of both X and Y directions!
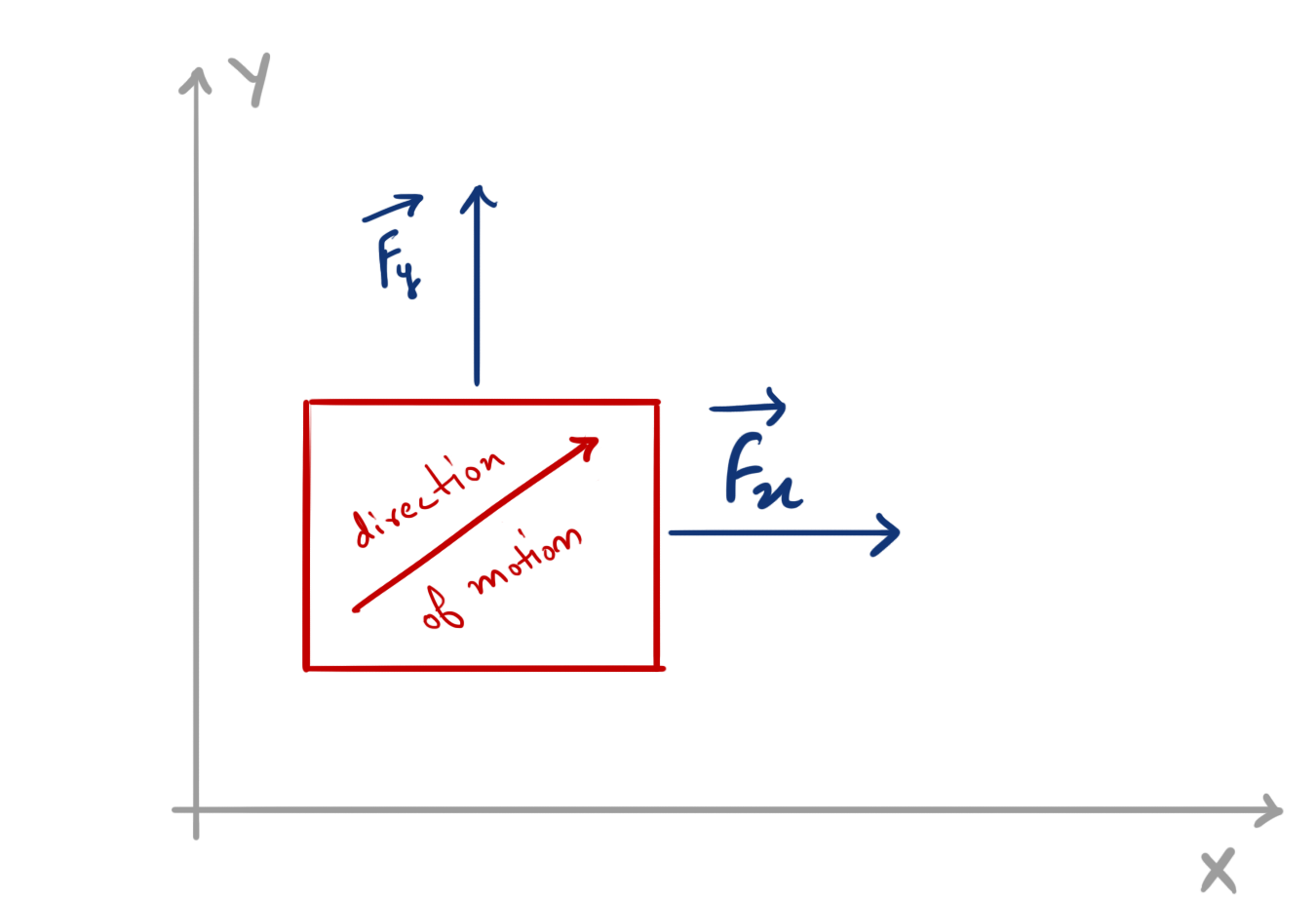
By applying forces \( \vec{F_x} \) and \( \vec{F_y} \) at the same time, we’re actually adding the forces together so that the body moves in the direction of the resultant of these forces.
Now, because the body is moving in a direction different than the direction of forces, It can be assumed that instead of forces \( \vec{F_x} \) and \( \vec{F_y} \), there’s a force of magnitude R acting on the body which makes the body move in its direction
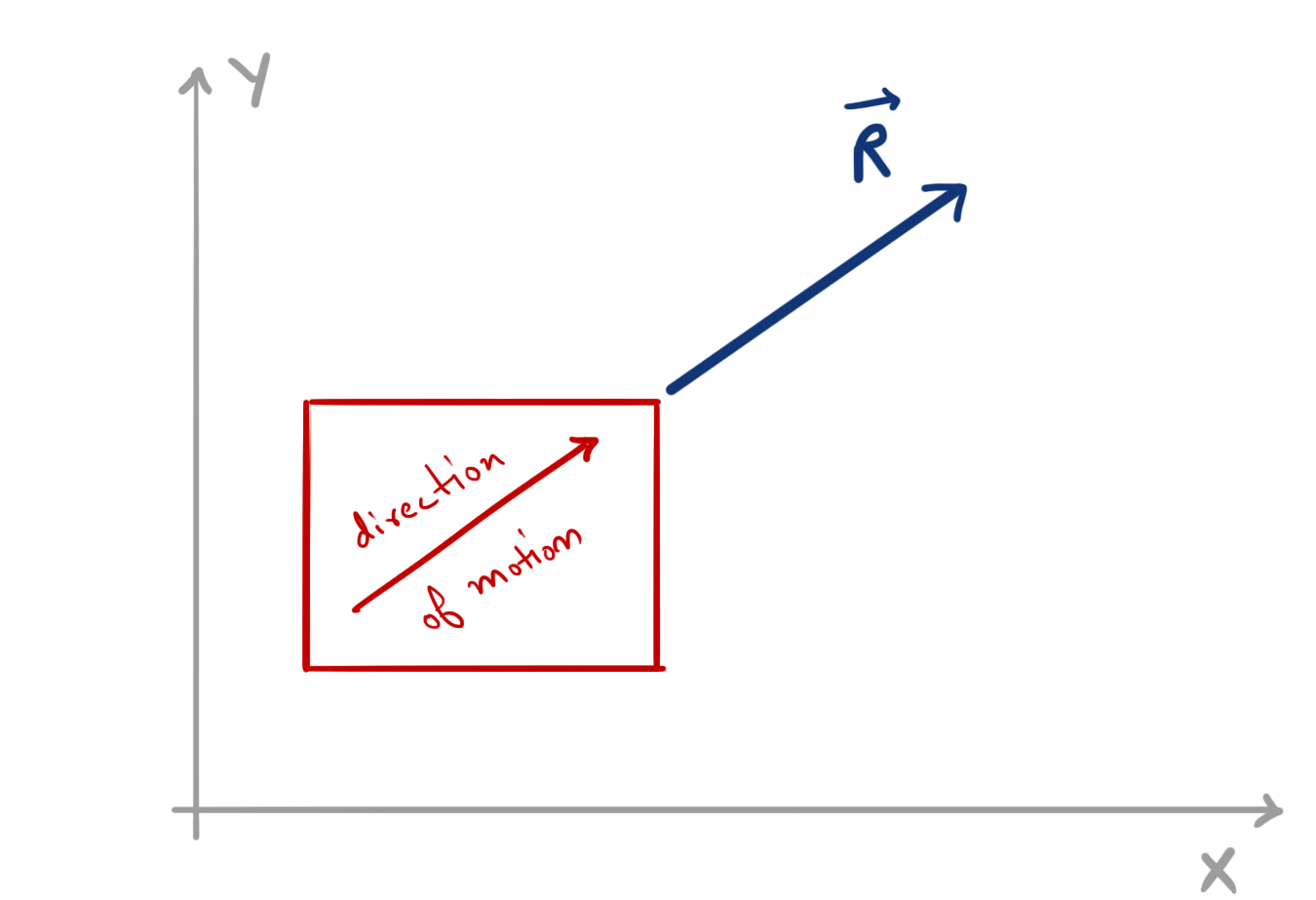
And this force \( \vec{R} \) is actually the resultant of forces \( \vec{F_x} \) and \( \vec{F_y} \)!
Hence, \( \vec{R}=\vec{F_x}+\vec{F_y} \)
Note that, the vector R is the resultant of “vector addition” of two forces. It is not equal to the addition of the magnitude of two forces.
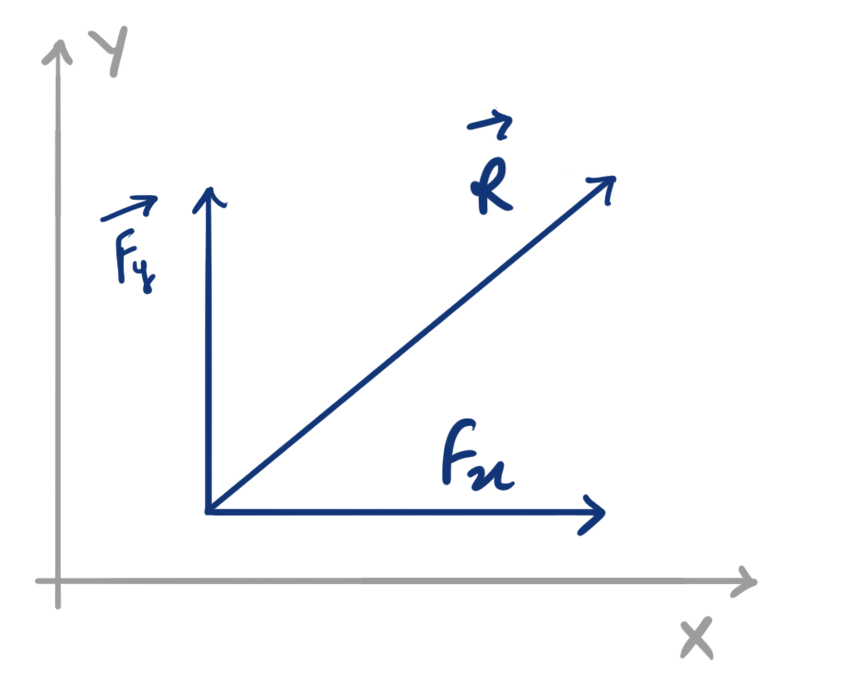
For this particular case, since the forces \( \vec{F_x} \) and \( \vec{F_y} \) has the direction along the X and Y axis, It can also be said that the forces \( \vec{F_x} \) and \( \vec{F_y} \) are the component forces of the Force \(\vec R\).
And that’s basically how the vector addition works (Remember, force is a vector quantity). But there comes another question!
Why is the Resultant of two vectors A and B drawn like this:
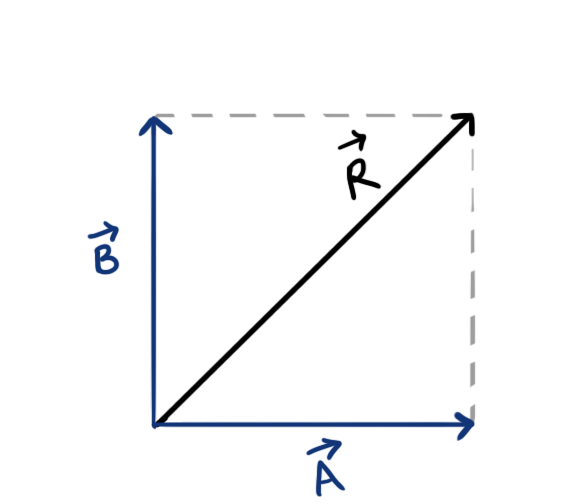
And not like this:
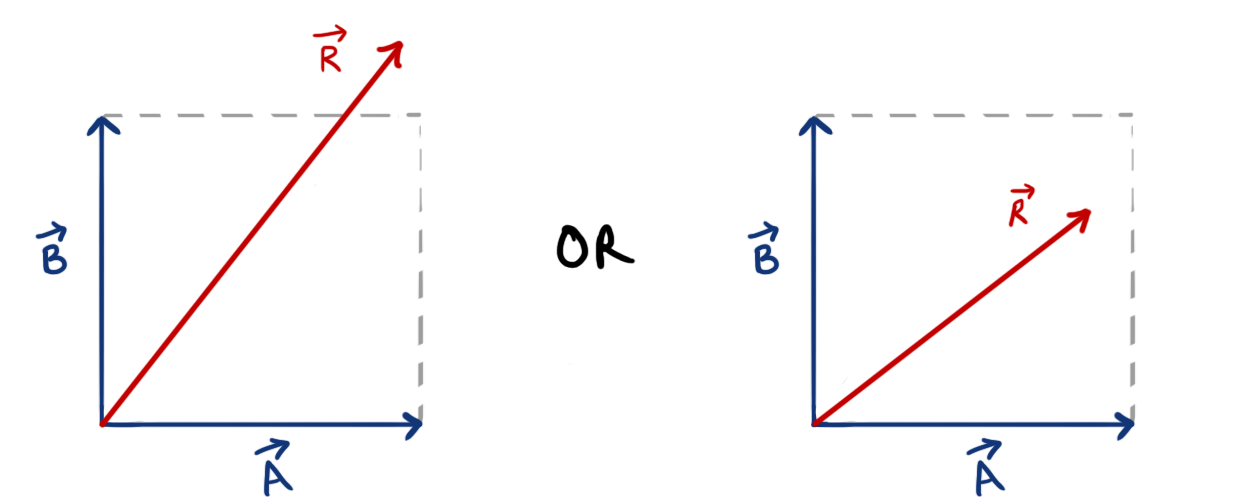
The answer is parallelogram law and triangle law of vectors.
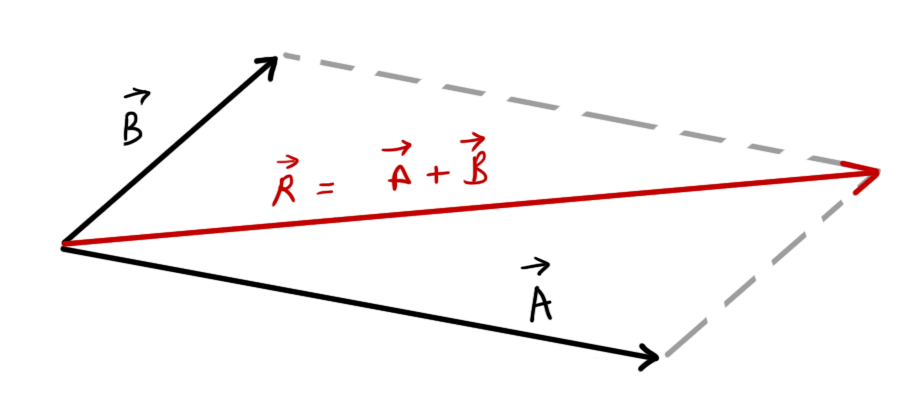
Parallelogram law of vectors
According to the parallelogram law of vectors, If we have two vectors A and B,
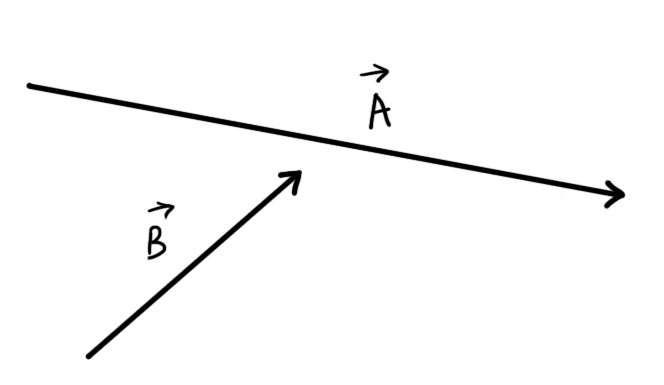
And if we parallel shift the two vectors in a way that both the vectors represent adjacent sides of a parallelogram, and, both of the vectors either direct away from or direct towards each other at the same time as shown in the figure:

Then, the diagonal of the parallelogram formed will be the resultant of the two vectors A and B.
Triangle law
Similar to the Parallelogram law of vectors, we also have triangle law of vectors. If we parallel-shift vector \(\vec{B}\) such that the tail of vector B touches the head of vector A as shown in figure
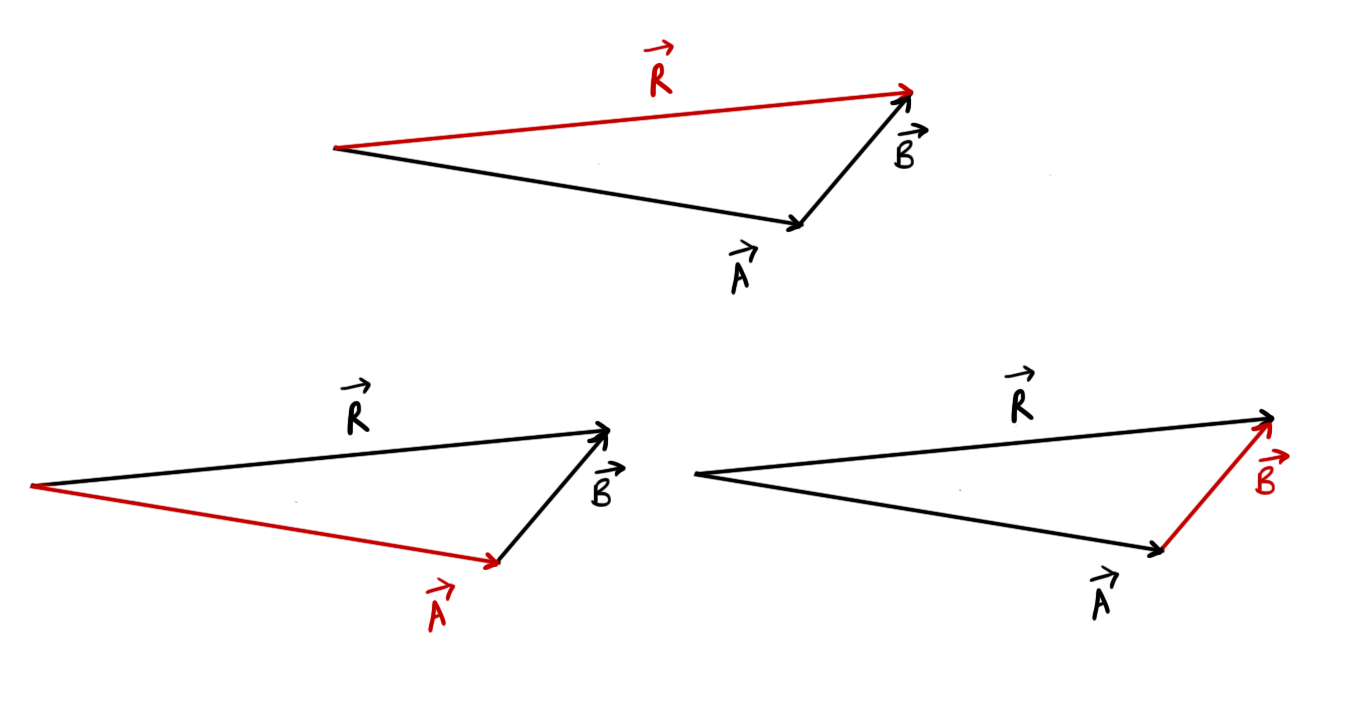
Then, according to the triangle law of vectors,
\[ \begin{aligned} &\vec{R}=\vec{A}+\vec{B}\\ \text{or}\ \ & \vec{A}=\vec{R}-\vec{B}\\ \text{or}\ \ &\vec{B}=\vec{R}-\vec{A} \end{aligned} \]
Now that we know what a vector addition, parallelogram law, and triangle law of vectors are, let’s move on to the types of vector additions.
Addition of two vectors when their direction and magnitude is known
If \( \hat{a}, A\) and \( \hat{b}, B\) are the direction and magnitude of vectors \(\vec A\) and \(\vec B\) respectively,
such that, \( \vec{A}=A\hat{a} \)
and \( \vec{B}=B\hat{b} \)
then \[ \vec{A}+\vec{B}=A\hat{a}+B\hat{b} \]
Addition of two vectors having the same direction
If both vectors have the same direction, then the resultant of these two vectors, of course, will also be in the same direction, but with the magnitude equal to the sum of the magnitude of the two vectors.
Hence if, \(\hat b = \hat a\)
then, \( \vec{A}+\vec{B}=\ A\hat{a}+B\hat{a}\)
or, \( \vec{A}+\vec{B} =\ \left(A+B\right)\hat{a} \)
Addition of Two vectors when their components are known
If \( A_xi,\ A_yj \) and \( B_xi,\ B_yj \) are the component vectors of the vector \(\vec A\), and \(\vec B\) respectively, Then the Resultant of vectors \( \vec{A}+\vec{B} \) will be equal to the resultant of sum of all their component vectors.
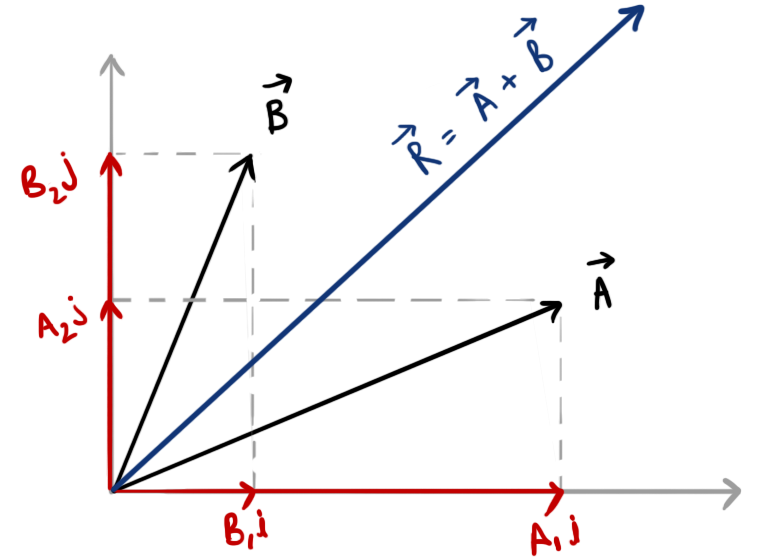
Hence, if \( \vec{A}=A_1i+A_2j \)
and \( \vec{B}=B_1i+B_2j \)
Then, \( \vec{A}+\vec{B}=A_1i+A_2j+B_1i+B_2j \)
or, \[ \vec{A}+\vec{B}=\left(A_1+B_1\right)i+\left(A_2+B_2\right)j \]
- Remember, Component vectors are just like normal vectors with direction along one of the reference axis (X, Y, or Z). So addition of component vectors is just similar to addition of vectors when their magnitude and direction is known.
- Notice how resultant R still follows the parallelogram law with A and B
Addition of two vectors when magnitude and angle between them is known
When we know the magnitude and angle made between two vectors, Parallelogram law can be applied to easily find the direction and magnitude of resultant vector.
Suppose, we had two vectors \( \vec{A}\text{ and } \vec{B} \) of magnitude \[A, B\] with an angle θ between them.
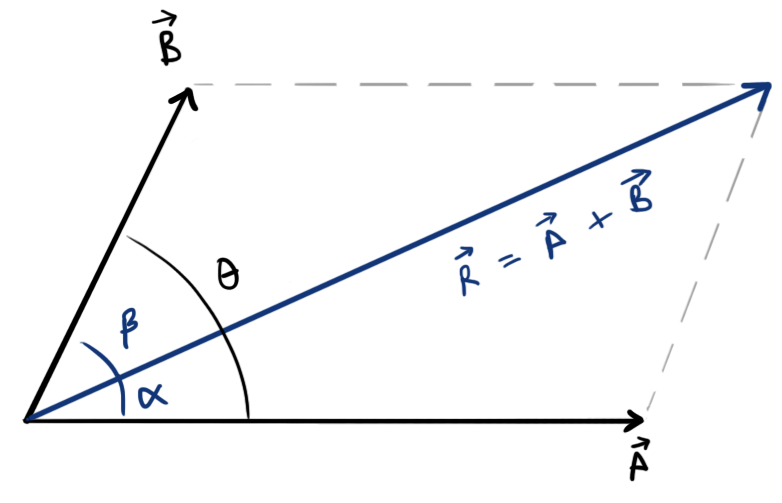
Then, with the help of parallelogram law,
\( \vec{R}=\vec{A}+\vec{B} \)
And the magnitude of \(\vec{R}\) will be equal to the length of the diagonal of the parallelogram,
\[ R=\sqrt{A^2+B^2+2AB\cos\theta} \]
and, if \(\alpha\) and \( \beta \) are the angle made by resultant R with A and B, then with the help of trigonometry, we have
\[ \alpha=\tan^{-1}\left[\frac{B\sin\theta}{A+B\cos\theta}\right] \]
similarly, \[ \beta=\left(\theta-\alpha\right)=\tan^{-1}\left[\frac{A\sin\theta}{B+A\cos\theta}\right] \]
Resultant of two orthogonal vectors
Two vectors are said to be orthogonal when they are perpendicular to each other.
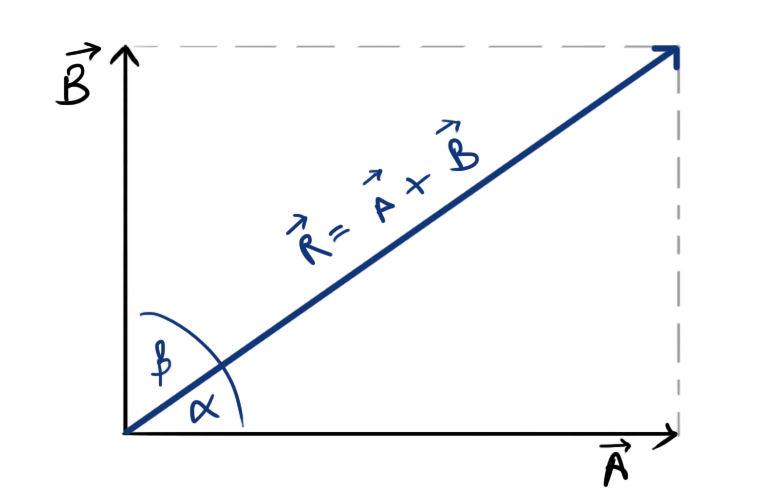
Hence, If the angle between \( \vec{A}\text{ and } \vec{B} \) is \[ 90^{\circ} \] and magnitude is A and B respectively, then by putting \[ \angle\theta=90^{\circ} \] in above equations,
magnitude, \( R=\sqrt{A^2+B^2} \)
and angle, \[ \alpha=\tan^{-1}\left[\frac{B}{A}\right] \]
- Addition of orthogonal vectors is similar to the magnitude of a vector whose components are known. And by now we should have a clear understanding of what components of vectors are.
Resolution of a vector in two directions
Just like we can add up two vectors to get a single resultant vector, We can also break (resolve) a single vector into two directions. This is called the Resolution of vector.
If \(\vec R\) is a vector of magnitude R and direction \(\hat r\), and we want to break it into two vectors \( \vec{A}\text{ and }\vec{B} \) which make angles \( \alpha\text{ and }\beta \) with \(\vec R\) as shown in figure, then the magnitude of vectors \( \vec{A}\text{ and }\vec{B} \) can be calculated by applying the opposite of parallelogram law.
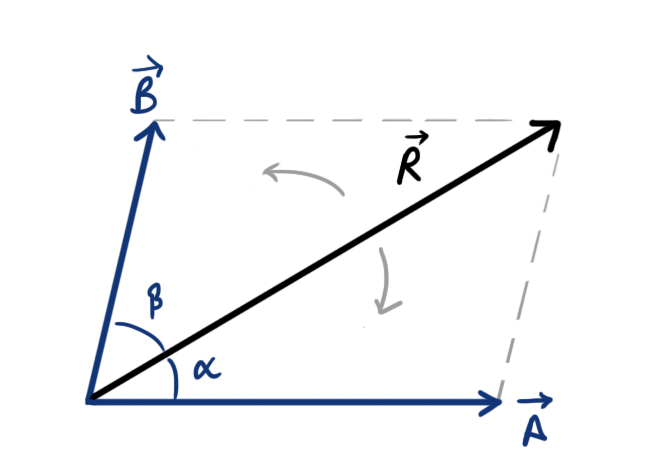
Hence, If \(\vec A \) makes angle \(\alpha\) and \(\vec B\) makes angle \(\beta\) with \(\vec R\)
then, \[ A=R\frac{\sin\beta}{\sin\left(\alpha+\beta\right)} \]
and, \[ B=R\frac{\sin\alpha}{\sin\left(\alpha+\beta\right)} \]
\(A\) and \(B\) are magnitude of vectors \(\vec{A}\) and \(\vec{B}\) respectively. And since we know the angles they make with \(\vec{R}\), Their direction is already known.
Resolution of a vector into two orthogonal vectors
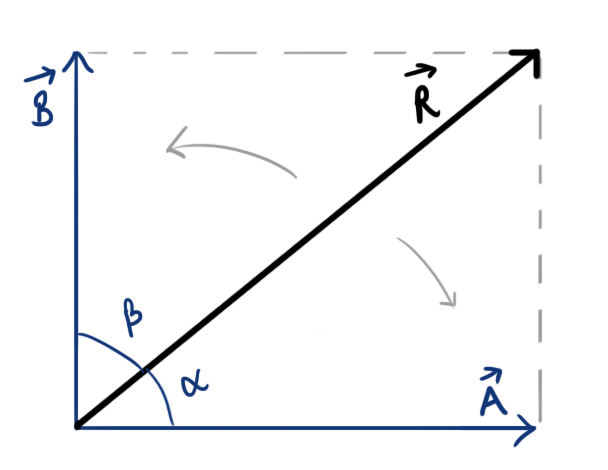
If \( \vec{A}\text{ and }\vec{B} \) are orthogonal, then by putting \[ \alpha+\beta=90^{\circ} \] in above two equations (or simply, with the help of trigonometric functions, as we did before to find magnitude of component vectors), we get
\[ A=R\cos\alpha\ =\ R\sin\beta \]
\[ B=R\sin\alpha\ =\ R\cos\beta \]
We’re doing great progress! We know what vectors and their components are, we known how vectors are added to get a resultant vector or broken into their components. On next page, we will talk about product of two vectors.
Next Part
This page is split into multiple parts.
- Vectors (Physics) | Part-1
- Vectors (Physics) | Part-2
