Data Structure Notes

Posted by Sajid Khan | Last updated on Dec 17th 2023

Classification of Data structure

Types of Data Strcutures with Related Algorithms:

Array DS

String

Heap

A complete binary tree data strcuture, where value of parent node >= children node. The comparison of values can be based on any kind of comparator.

• Max heap: Value of parent node >= value of children node
• Min heap: Value of parent node <= value of children node
• Since it’s a complete binary tree, heap can be easily implemented on simple arrays, because zero based index of left and right children of any node having index \( i \) can be calculated as \( 2i+1 \) and \( 2i+2 \)
• heapify() is the main function used in heaps, this is usually a recursive function

Stack

• Supports push, pop, peek operations
• Java has LinkedList<Object> class to perform stack operation. push, pop, and peek methods can be used to perform stack operations

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

    private static int[] minimumInPreviousK(int[] arr, int k) {
        int result[] = new int[arr.length];
        LinkedList<int[]> ms = new LinkedList<>();
        for (int i = 0; i < arr.length; i++) {
            while (!ms.isEmpty() && ms.peekFirst()[1] < i - k)
                ms.removeFirst();
            while (!ms.isEmpty() && ms.peekLast()[0] >= arr[i])
                ms.removeLast();
            ms.addLast(new int[]{arr[i], i});
            result[i] = ms.peekFirst()[0];
        }
        //result[] is an array where result[i] = min(result[i], result[i - 1], result[i - 2] ... result[i - k])
        return result;
    }

Priority Queue

• supports Queue/Deque (or Offer/Poll). Both have time complexity \( O\left(\log n\right) \).
• Maintains elements in sorted form at all time, whenever deque is performed, the first element of sorted list is returned.
• Access of sorted elements using index is not supported. For eg. accessing K_th smallest/largest element in the Priority Queue is not possible without deque-ing the first K-1 smallest/largest elements from queue.
• Usually Implemented using Heaps.
• Java has PriorityQueue<T> implemented in java.util package.

class MyObj {
    public int val;
    MyObj (int val) {
        this.val = val;
    }
}

MyObj obj1 = new MyObj(4);
MyObj obj2 = new MyObj(2);

PriorityQueue<MyObj> pq = new PriorityQueue<>((x, y) -> Integer.compare(x.val, y.val));

pq.offer(obj1);
pq.offer(obj2);

System.out.println(pq.peek().val); // prints 2, as 2 is the smallest element

obj2.val = 6; //value of object is modified with the help of reference variable, the priority queue will not be re-sorted

System.out.println(pq.peek().val); // prints 6, however 6 is not the smallest element

class MyObj {
    public int val;
    MyObj (int val) {
        this.val = val;
    }
}

MyObj obj1 = new MyObj(4);
MyObj obj2 = new MyObj(2);

PriorityQueue<MyObj> pq = new PriorityQueue<>((x, y) -> Integer.compare(x.val, y.val));

pq.offer(obj1);
pq.offer(obj2);

System.out.println(pq.peek().val); // prints 2, as 2 is the smallest element

pq.remove(obj2); //remove old value (takes O(n))
obj2.val = 6;   // update
pq.offer(obj2); // add again

System.out.println(pq.peek().val); // prints 4 now, which is also the smallest elementt

class MyObj {
    public boolean obsolete = false; // by default, the object is not obsolete
    public int val;
    MyObj (int val) {
        this.val = val;
    }
}

MyObj obj1 = new MyObj(4);
MyObj obj2 = new MyObj(2);

PriorityQueue<MyObj> pq = new PriorityQueue<>((x, y) -> Integer.compare(x.val, y.val));

pq.offer(obj1);
pq.offer(obj2);

System.out.println(pq.peek().val); // prints 2, as 2 is the smallest element

obj2.obsolete = true;       //mark the old object instance as obsolete
obj2 = new MyObj(6);    //create new object instance with updated value
pq.offer(obj2);             //add the new object instance

//The following loop should always be used before performing the peek() operation on priority queue
//The following loop executes at most 'm' iterations in total, where m is the number of updates made to objects in priority queue
//therefore, this while loop executes only one iteration for each update
//that means, this while loop can be considered O(log(n)) for each update performed where O(log(n)) is time taken by method poll()
while (!pq.isEmpty() && pq.peek().obsolete) pq.poll();

System.out.println(pq.peek().val); // prints 4 now, which is also the smallest element

class MyObj {
    public int val;
    MyObj (int val) {
        this.val = val;
    }
}

Set<MyObj> isObsolete = new HashSet<>();// use HashSet to store the obsolete property of object

MyObj obj1 = new MyObj(4);
MyObj obj2 = new MyObj(2);

PriorityQueue<MyObj> pq = new PriorityQueue<>((x, y) -> Integer.compare(x.val, y.val));

pq.offer(obj1);
pq.offer(obj2);

System.out.println(pq.peek().val); // prints 2, as 2 is the smallest element

isObsolete.add(obj2);       //this suggests that old instance of obj2 is not obsolete
obj2 = new MyObj(6);    //create new object instance with updated value
pq.offer(obj2);             //add the new object instance

//The following loop should always be executed before performing the peek() operation on priority queue
//The following loop executes at most 'm' iterations in total, where m is the number of updates made to objects in priority queue
//therefore, this while loop executes only one iteration for each update
//that means, this while loop can be considered O(log(n)) for each update performed where O(log(n)) is time taken by method poll()
while (!pq.isEmpty() && isObsolete.remove(pq.peek())) pq.poll();
//pay attention to the remove() method call made above, this frees the memory as long as it is no longer needed
    
System.out.println(pq.peek().val); // prints 4 now, which is also the smallest element

class MyObj {
    public int val;
    MyObj (int val) {
        this.val = val;
    }
}

MyObj obj1 = new MyObj(4);
MyObj obj2 = new MyObj(2);

TreeSet<MyObj> ts = new TreeSet<>((x, y) -> Integer.compare(x.val, y.val));

ts.add(obj1);
ts.add(obj2);

System.out.println(ts.first().val); // prints 2, as 2 is the smallest element
obj2.val = 6; //object 6 has been modified, however this doesn't re-sorts the tree set
System.out.println(ts.first().val); // prints 6, the updated value of object, which is not the smallest element


obj2.val = 2; // restore the value, so that tree set can identify it again
ts.remove(obj2); //removes obj2 in O(logN) time
obj2.val = 6; //modify the value
ts.add(obj2); //adds obj2 again to trigger re-sorting
System.out.println(ts.first().val);//prints 4 now, which is now the smallest element

Graph

• Collection of nodes connected together with edges.
  • Directed Graph: Direction of edges matter.
  • Undirected or Bidirected Graph: Direction of edges doesn’t matter.
  • Cyclic Graph: Graph that contains cycles (loops).
  • Acyclic Graph: Graph doesn’t contain cycles.
  • Direct Acyclic Graph: A directed graph which does not contain cycles when traversing through edges respecting the direction of edges. The graph however may contain cycles when direction of edges is not considered.
  • Connected Graph: All nodes are connected, there is only one group, every node is reachable from every other node in the graph.
  • Disconnected Graph: All nodes are not connected, there can be multiple groups of nodes.
  • Weighted graph: Each edge is associated with some value/cost.
  • Complete Graph: A graph in which each pair of vertices are connected with a single edge. (Every possible edge exists). A complete graph with \( n \) vertices has \[ \frac{n\left(n-1\right)}{2} \] edges.
  • Diameter of Graph: The greatest minimum distance between any pair of vertices in a graph. In other words, two find diameter of graph -> find shortest distance between each pair of vertices of graph -> the maximum of those distances is the diameter of graph.
  • Bipartite Graph: A graph in which nodes can be divided into two groups such that every edge connecting the nodes are also divided into to parts. I.e, graph is bipartite if it’s possible to divide graph in two groups, such that for each edge in the graph, the two endpoints of the edge lie in different groups.
    • All Acyclic graph are Bipartite graph
    • A cyclic graph is Bipartite if, each cycle of the graph has even length (even number of edges).
  • Isomorphic Graphs: Two graphs are Isomorphic if both of them are structurally the same. Position of nodes doesn’t matter, as long as structure of two graphs are same.
  • In-degree of a node: The number of incoming edges attached to the node.
  • Out-degree of a node: The number of outgoing edges attached to the node.

Graph Algorithms

• Union Find algorithm: Also called Disjoint Set Union (DSU) algorithm
  • Used to find groups in graph. Each group is represented by it’s representative node.
  • Implementation contains two functions union() and find()

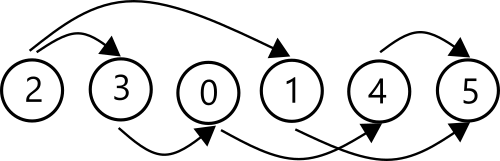
• Topological Sorting of graph: Sorting the nodes of graph in a way such that, when nodes are placed linearly one after another, the direction of all edges are from left to right.
  • A single graph can be topologically sorted in multiple ways. (non-unique solution)
  • Use case: Program build dependency, Course prerequisite completion
  • Topological Sort Algorithms:

DFS for topological sort. O(n) time O(n) space

• Create global visited[node] array
• Create global result[] array
• Perform DFS on each node
  • For current node in DFS, find all it’s outgoing nodes which are not in visited[node]. Perform DFS on those nodes.
  • After performing DFS on all it’s outgoing nodes, Add current node to result[] array
• Reverse result[] array
• Tutorial Link

Kahn’s Algorithm for topological sort. O(n) time O(n) space

• Create global indegree[node] hashmap and global result[] array.
• Queue all nodes with zero in-degree.
• While Queue is not empty:
  • Poll single node, push it to result array
  • Update indegree[outgoing nodes]. (Subtract 1 from each outgoing node of currently polled node)
  • If new in-degree of any outgoing node becomes zero, add this outgoing node to queue.
• result[] array is topologically sorted

• Single source shortest path (SSSP): For any given node, find shortest path/distance of all other nodes from given node.
  • Used with weighted direct acyclic graphs (DAG)
  • TODO: SSSP algorithms: Dijkstra, bellman ford, floyd warshall
• Minimum Spanning Tree:
  • TODO: Krukshal algorithm, Prim’s algorithm

Graph Problems

1. Check if graph is bipartite: Can be achived by checking if graph is acyclic. In case if graph is found to be cyclic, making sure that each cycle has even number of edges. This can be achived by DFS as well as BFS
2. Find Center or Diameter of acyclic undirected graph (Tree): Center of undirected acyclic graph (Tree) is the center node which falls under the longest path in the Tree (undirected acyclic graph). The longest path is called diameter of the Tree.

Two approaches to find center of Tree

1. Queue all the leaf nodes/vertices of the graph. Delete them one by one and keep adding newly formed leaf nodes to queue until a single node is left in the queue, which is the center of the Tree.
   Time and space complexity: \( O\left(n\right) \)
2. Use recursion to find two end nodes of the longest path. and then recursion again to find the middle path.
   Time complexity: \( O\left(n\right) \), Space complexity: \( O\left(1\right) \)
   This solution uses this technique to find center of tree, however, after finding two end nodes of the tree, the code uses an array to figure out the center of the longest parth. Using array can be avoided and center can be figured out without extra space (ignoring the space used for recursion).

• TODO: Check if two graphs are isomorphic.

Tree

Trees are Acyclic connected Graph where any node of the graph can be represented as Root of the tree.

Rooted Tree: Directed acyclic connected graph, where direction of edges start from root of tree to the end/leaf node of tree.

Segment Tree

• Binary (usually) tree based data structure used to store information of ranges as well as perform operations on the ranges of the arrays. Any array can be broken into multiple segments/ranges and information of these ranges can be stored in a binary tree where each node accounts for storing information of some range of the array in binary tree fashion.
• A simple and general implementation of segment tree is used for querying sum/min/max of range of array in O(logN) and do the point updates of values of array in O(logN) time.
• Segment tree works with ranges which are additive in nature, i.e. if \( f\left(a,b\right) \) is value of range \( a \) to \( b\), and \( f\left(c,d\right) \) is value of range \( c \) to \( d \), then \( f\left(a,d\right)=f\left(a,b\right)+f\left(c,d\right) \) should satisfy.
• Segment tree is better when frequent query as well as updates are performed. Otherwise prefix sum can be used just to get range sum in constant time.
• Segment tree are also used to calculate GCD/LCM of range of arrays.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

//Range Sum Segment Tree
class St {
    private int low, high, val;
    private St left, right;
    
    //constructor 1 : build a dummy segment tree of fixed length/range.
    //the segment tree can be populated later by calling pointUpdate() for each index
    public St(int low, int high) {
        this.low = low;
        this.high = high;
        this.val = 0;
        
        if (low == high)
            return;
        
        int mid = low + (high - low) / 2;
        
        this.left = new St(low, mid);
        this.right = new St(mid + 1, high);
    }

    //constructor 2 : build and populate segment tree on the go, by passing array to constructor
    public St(int arr[], int low, int high) {
        this.low = low;
        this.high = high;
        if (low == high) {
            this.val = arr[low];
            return;
        }
        int mid = low + (high - low) / 2;
        this.left = new St(arr, low, mid);
        this.right = new St(arr, mid + 1, high);
        this.val = this.left.val + this.right.val;
    }

    public void pointUpdate(int idx, int val) {
        if (this.low > idx || this.high < idx)
            return;
        if (this.low == this.high) {
            this.val = val;
            return;
        }

        this.left.pointUpdate(idx, val);
        this.right.pointUpdate(idx, val);

        this.val = this.left.val + this.right.val;
    }
    public void pointAdd(int idx, int addVal) {
        if (this.low > idx || this.high < idx)
            return;
        if (this.low == this.high) {
            this.val += addVal;
            return;
        }
        
        this.left.pointAdd(idx, addVal);
        this.right.pointAdd(idx, addVal);

        this.val = this.left.val + this.right.val;
    }
    public int rangeSum(int queryLow, int queryHigh) {
        if (queryLow > this.high || queryHigh < this.low)
            return 0;
        if (queryLow <= this.low && queryHigh >= this.high)
            return this.val;
        return this.left.rangeSum(queryLow, queryHigh) + this.right.rangeSum(queryLow, queryHigh);
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

//Range Sum Segment Tree
class St {
    private int st[], length;
    
    public St(int arr[]) {
        length = arr.length;
        st = new int[length * 4]; //maximum length of segment tree can be 4 times of original array
        build(arr, 0, 0, arr.length - 1);
    }

    public void build(int arr[], int nodeIdx, int curLow, int curHigh) {
        if (curLow == curHigh) {
            st[nodeIdx] = arr[curLow];
            return;
        }
        int mid = curLow + (curHigh - curLow) / 2;
        int left = nodeIdx * 2 + 1;
        int right = left + 1;
        build(arr, left, curLow, mid);
        build(arr, right, mid + 1, curHigh);
        st[nodeIdx] = st[left] + st[right];
    }

    public void pointUpdate(int idx, int val) {
        pointUpdate(idx, val, 0, 0, length - 1);
    }
    public void pointUpdate(int arrIdx, int val, int nodeIdx, int curLow, int curHigh) {
        if (curLow > arrIdx || curHigh < arrIdx)
            return;
        if (curLow == curHigh) {
            st[nodeIdx] = val;
            return;
        }
        int mid = curLow + (curHigh - curLow) / 2;
        int left = nodeIdx * 2 + 1;
        int right = left + 1;
        pointUpdate(arrIdx, val, left, curLow, mid);
        pointUpdate(arrIdx, val, right, mid + 1, curHigh);
        st[nodeIdx] = st[left] + st[right];
    }

    public void pointAdd(int idx, int addVal) {
        pointAdd(idx, addVal, 0, 0, length - 1);
    }
    public void pointAdd(int arrIdx, int addVal, int nodeIdx, int curLow, int curHigh) {
        if (curLow > arrIdx || curHigh < arrIdx)
            return;
        if (curLow == curHigh) {
            st[nodeIdx] += addVal;
            return;
        }
        int mid = curLow + (curHigh - curLow) / 2;
        int left = nodeIdx * 2 + 1;
        int right = left + 1;
        pointAdd(arrIdx, addVal, left, curLow, mid);
        pointAdd(arrIdx, addVal, right, mid + 1, curHigh);
        st[nodeIdx] = st[left] + st[right];
    }

    public int rangeSum(int low, int high) {
        return rangeSum(low, high, 0, 0, length - 1);
    }
    public int rangeSum(int queryLow, int queryHigh, int nodeIdx, int curLow, int curHigh) {
        if (curLow > queryHigh || curHigh < queryLow)
            return 0;
        if (curLow >= queryLow && curHigh <= queryHigh) {
            return st[nodeIdx];
        }
        int mid = curLow + (curHigh - curLow) / 2;
        int left = nodeIdx * 2 + 1;
        int right = left + 1;
        return
            rangeSum(queryLow, queryHigh, left, curLow, mid) +
            rangeSum(queryLow, queryHigh, right, mid + 1, curHigh);
    }

}

Fenwick Tree (Binary Indexed Tree / BIT)

• Fenwick Tree, also called Binary Indexed Tree (BIT) are used to store information of ranges of arrays as well as perform operations on those ranges of the arrays.
• Fenwick trees work with the ranges where value of range can be deduced by subtracting two values of bigger ranges. I.e. if \( f\left(a,b\right) \) is value of range \( a \) to \( b\), and \( f\left(a,c\right) \) is value of range \( a \) to \( c \) then, the value of range b to c can be calculated based on the formula \( f\left(b,c\right)=f\left(a,c\right)-f\left(a,b\right) \)
• Common use of Fenwick tree is range sum queries with point updates on the array. However Range minimum/maximum query (RMQ) can’t be implemented since information stored in ranges for these kind of queries don’t have subtractive nature.
• General implementation of Fenwick tree works with 1 based indexes, however slight modification can be made to make it work with 0 based indexes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

// BIT with 0 based index implementation
class BIT {
    private int bit[]; //store prefix sum
    private int arr[]; //store actual array
    
    public BIT (int arr[]) {
        this.arr = new int[arr.length];
        bit = new int[arr.length];
        for (int i = 0; i < arr.length; i++)
            pointUpdate(i, arr[i]);
    }

    public void pointUpdate(int i, int newVal) {
        pointAdd(i, newVal - arr[i]);
    }

    public void pointAdd(int i, int addVal) {
        if (i < 0) return;
        arr[i] += addVal;
        i++; //internally convert to 1 based index to perform required calculations
        while (i <= bit.length) {
            bit[i - 1] += addVal;
            i += lowestBit(i);
        }
    }

    public int preffixSum(int i) {
        i++; //internally convert to 1 based index to perform required calculations
        int sum = 0;
        while (i >= 1) {
            sum += bit[i - 1];
            i -= lowestBit(i);
        }
        return sum;
    }

    public int rangeSum(int low, int high) {
        return preffixSum(high) - preffixSum(low - 1);
    }

    private int lowestBit(int n) {
        return n & -n;
    }
}

Sorted Set (Tree Set)

Dynamic Programming with multiple state variables

Note: This is NOT multi-dimentional DP

In Multi-state DP problems, the solution of a problem in one state is derived from the solution of subproblem in another state. For eg, to find the maximum profit made by selling a stock at day \( d \) by trading stock can be derived by knowing the maximum avialable balance present after buying the stock in previous days, here buying and selling are two states of the problem.

Boyer Moore’s Majority Voting Algorithm

Boyer Moore’s Majority Voting algorithm is used to find the majority element. A majority element is an element in array which repeats more than half the length of the array.