Vectors (Physics)
Posted by Sajid Khan | Last updated on
This page is split into multiple parts.
- Vectors (Physics) | Part-1
- Vectors (Physics) | Part-2
Product of Vectors
Vector multiplication is a lot different than the simple multiplication (of two scalar quantities). We not only have to think about the multiplication of their magnitudes but also of their directions (Which doesn’t really make sense).
Before we talk about how a vector is multiplied by another vector, let’s first talk about what happens when a scalar quantity (simply a number) is multiplied by a vector quantity.
Product of a vector and a scalar
Multiplication of a vector by a scalar (a number) have two cases:
Multiplication of Vector with a Positive number
When a vector is multiplied by a positive number (greater than 0), only the magnitude of the vector gets multiplied by the number, but the direction of vector remains unchanged.
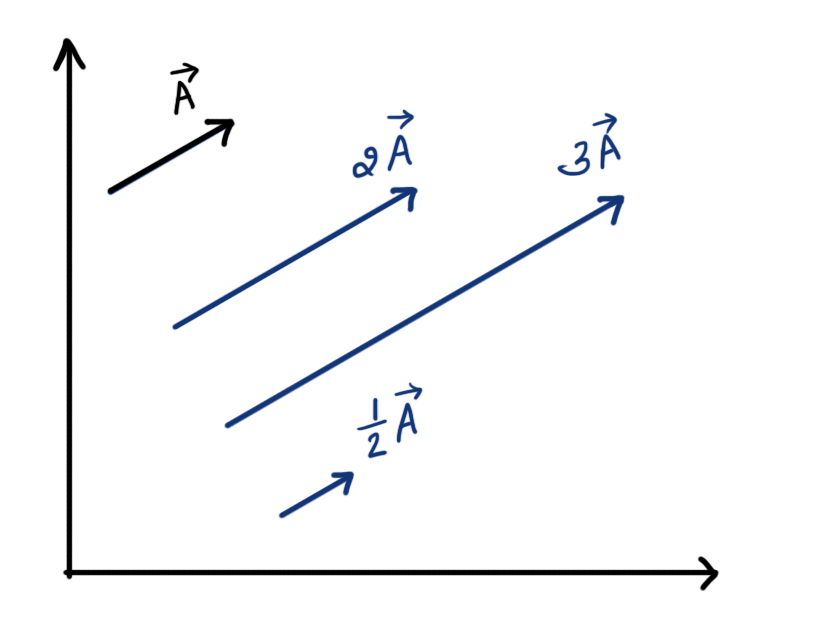
Thus, if \(\vec A\) is a vector of magnitude A and direction \(\hat a\)
\( \vec{A}=A\hat{a} \)
Then, the product of vector A with a number \(n\) will be given as
\( n\times\vec{A}=n\times A\hat{a} \)
or, \[ n\times\vec{A}=\left(nA\right)\hat{a} \]
Note that the \( \times \) symbol here represents a simple multiplication, Don’t confuse it with the “Cross product” which we’ll talk about in upcoming sections.
Multiplication of vector with a negative number
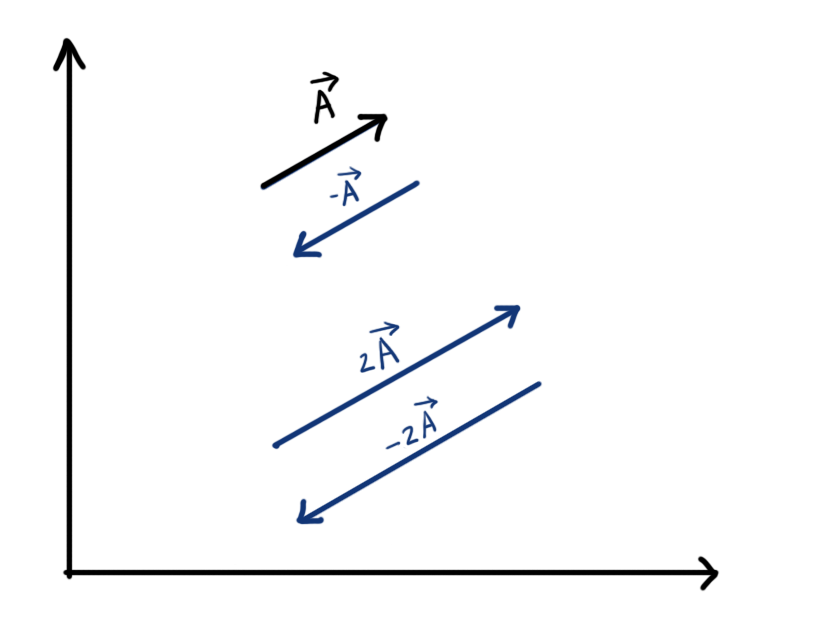
When a vector is multiplied by a negative number (less than 0), Magnitude of the vector gets multiplied by the number, and the direction of the vector gets reversed.
Following are some important points to remember when multiplying a vector with a scalar:
- Multiplication of a vector with a number is distributive
\[ \begin{aligned} &n(\vec{A}+\vec{B}) = n\vec{A}+n\vec{B} \\ \text{and, }\ &n_1\vec{A}+n_2\vec{A} = \left(n_1+n_2\right)\vec{A} \end{aligned} \] - Multiplication of vector with number is Commutative
\( n\vec{A}=\vec{A}n \) - The product remains unchanged when a vector is multiplied by 1
\( 1\times\vec{A}=\vec{A} \) - When a vector is multiplied by -1, the length of the line representing the vector remains same but the direction of vector is reversed
- Multiplying a vector by 0 results in a zero vector. A zero vector is a vector whose magnitude is zero
\( 0\times\vec{A}=\vec{0} \)
The magnitude of components of a zero vector is 0
\( \vec{0}=0i+0j+0k \)
And finally, here we are at the last part of this tutorial!
Product of Vector with Vector
Just think of how a vector (which has both, magnitude as well as direction) can be multiplied by another vector?
You probably may think of many ways that you could put it together, But to get its best use in many circumstances, the product of two vectors is defined in two ways.
(1) The Dot product (also called the scalar product), and (2) The Cross product (also called the vector product)
Dot Product (Scalar Product)
Dot product is that product of two vectors, In which the magnitude of first vector is multiplied by the magnitude of “Projection of second vector onto the first vector”.
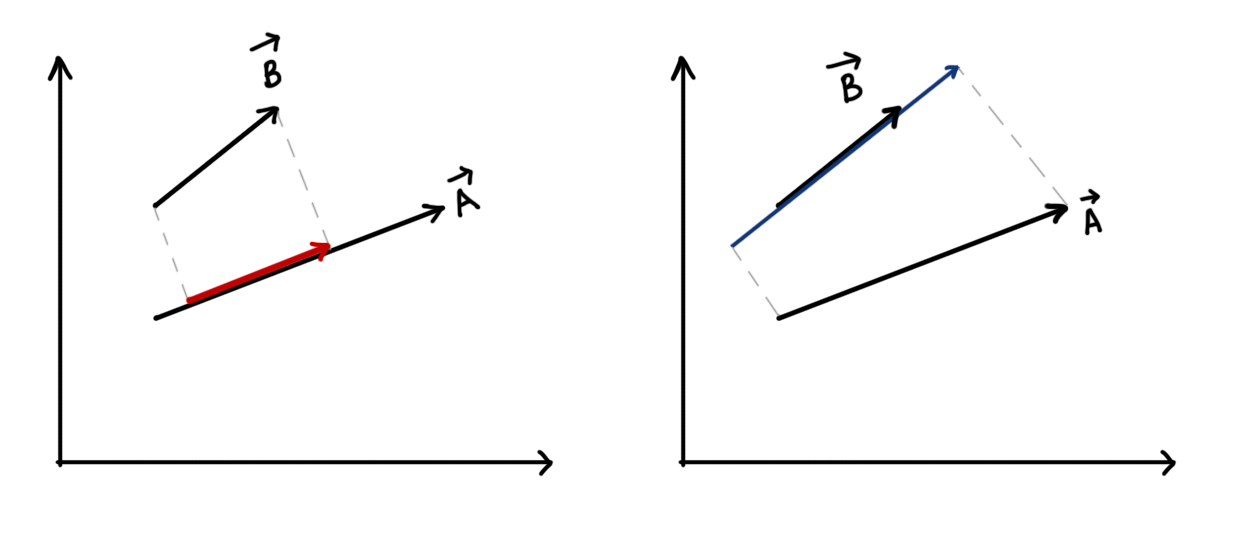
For vector A and B as shown in the image above, Red line represents the projection of vector B onto vector A, and the Blue line represents the Projection of vector A onto vector B
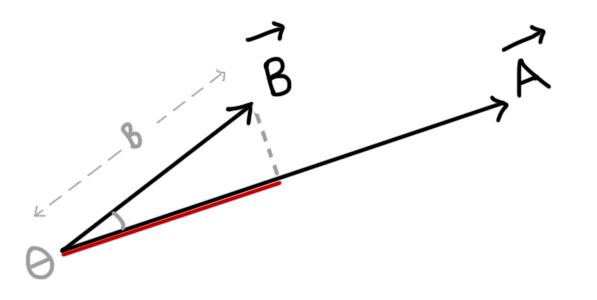
If we parallel-shift vector A and B in a way so that they meet each other at the endpoint, then, The magnitude of projected lines can be calculated with the help of trigonometric functions.
So if the angle between the two vectors is θ, then
Magnitude of projection of \(\vec B\) onto \(\vec A \ =\ B\cos\theta \)
similarly, Magnitude of projection of \(\vec A\) onto \(\vec B\ = \ A\cos\theta \)
Note: Dot product of two vectors is represented by putting a Dot between the two vectors.
Hence, If \(\vec A\) and \(\vec B\) are two vectors of magnitude \(A\) and \(B\)
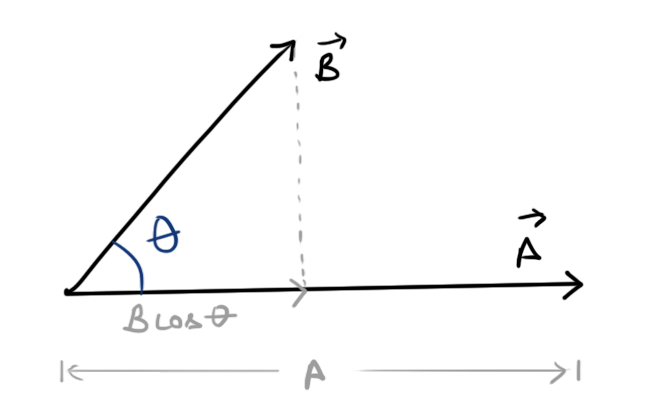
Then the Dot product of vector A and B is given as
\( \vec{A}\cdot\vec{B}=\left(A\cos\theta\right)B \) (\( A\cos\theta \) is magnitude of projection of vector A onto vector B)
or, \( \vec{A}\cdot\vec{B}=A\left(B\cos\theta\right) \) (\( B\cos\theta \) is magnitude of projection of vector B onto vector A)
Or, just simply \[\vec{A}\cdot\vec{B}=AB\cos\theta \] (Equation 1)
- The result of Dot product of two vectors is a Scalar quantity (a number).
- Dot product of orthogonal vectors (perpendicular to each other) is zero. (Because projection of a vector onto another vector is zero if both vectors are perpendicular to each other)
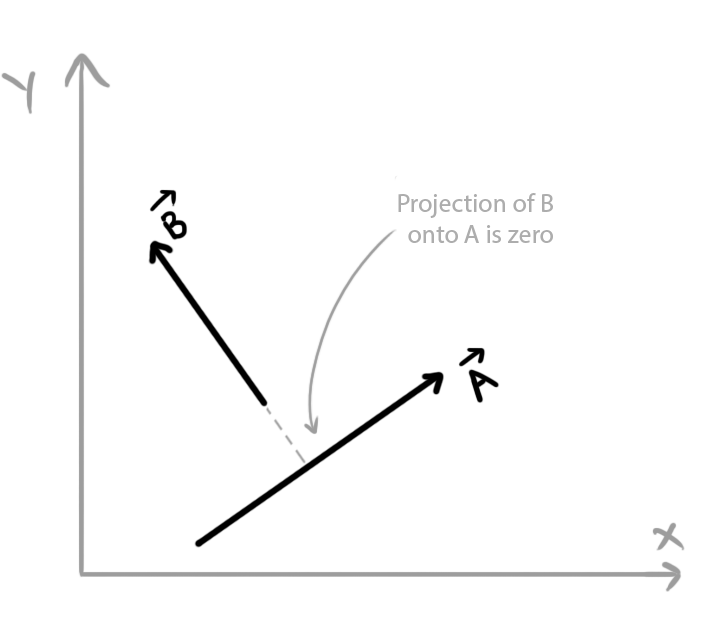
Or alternatively, by putting \[ \theta=90^{\circ} \] in equation 1,
\[ \vec{A}\cdot\vec{B}=AB\cos90^{\circ}=0 \] - Because \( i,\ j,\ \text{and }k \) represent unit vectors with direction parallel to X, Y, and Z axis respectively,
then, \( i\ \perp\ j\ \perp\ k \)
hence, \[ i\cdot j=j\cdot k=k\cdot i=0 \] - Dot product of two vectors having same direction is simply the product of their magnitude
\[Ai\cdot Bi=AB\cos0^{\circ}=AB \]
Dot product of two unit vectors having same direction is unity (equal to one)
\( \hat{a}\cdot\hat{a}=1 \)
similarly, \( i\cdot i=j\cdot j=k\cdot k=1 \) - Dot product is commutative
\( \vec{A}\cdot\vec{B}=\vec{B}\cdot\vec{A} \) - Dot product is associative
\( \vec{A}\cdot\vec{B}\cdot\vec{C}=\vec{A}\cdot\left(\vec{B}\cdot\vec{C}\right)=\left(\vec{A}\cdot\vec{B}\right)\cdot\vec{C} \) - Dot product is distributive
\( \vec{A}\cdot\left(\vec{B}+\vec{C}\right)=\vec{A}\cdot\vec{B}+\vec{A}\cdot\vec{C} \)
Algebraic definition of Dot product
Algebraically, If \( \vec{A}=A_1i+A_2j+A_3k \)
and, \( \vec{B}=B_1i+B_2j+B_3k \)
then, the dot product of vector A and B is given as
\( \vec{A}\cdot\vec{B}=\left(A_1i+A_2j+A_3k\right)\cdot\left(B_1i+B_2j+B_3k\right) \)
since dot product is distributive,
\[ \begin{aligned} \vec{A}\cdot\vec{B} = &\left(A_1i\cdot B_1i\right)+\left(A_1i\cdot B_2j\right)+\left(A_1i\cdot B_3k\right)+\\ &\left(A_2j\cdot B_1i\right)+\left(A_2j\cdot B_2j\right)+\left(A_2j\cdot B_3k\right)+\\ &\left(A_3k\cdot B_1i\right)+\left(A_3k\cdot B_2j\right)+\left(A_3k\cdot B_3k\right) \end{aligned} \]
and because i, j, and k are orthogonal, \( i\cdot j=j\cdot k=k\cdot i=0 \)
also, \[ A_1i\cdot B_1i=A_1B_1\cos0^{\circ}=A_1B_1 \]
\( A_2j\cdot B_2j=A_2B_2 \)
\( A_3k\cdot B_3k=A_3B_3 \)
Putting above equations together, We get
\[ \vec{A}\cdot\vec{B}=A_1B_1+A_2B_2+A_3B_3 \] (Equation 2)
Some applications of Dot Product
- For two vectors A and B of known components
\( \vec{A}=A_1i+A_2j+A_3k \)
\( \vec{B}=B_1i+B_2j+B_3k \)
With the help of equation 1 and equation 2 Dot Product can be used to easily calculate the angle between these two vectors
\( AB\cos\theta=A_1B_1+A_2B_2+A_3B_3 \)
\[ \theta=\cos^{-1}\left[\frac{A_1B_1+A_2B_2+A_3B_3}{AB}\right] \]
where \(A\) and \(B\) are magnitude of vector A and B - When angle between two vectors is not known, with the help of equation 1 and equation 2, Dot product can be used to calculate magnitude of projection of one vector onto another vector.
- Dot product is used to test whether the two vectors are perpendicular to teach other or not
If, \( \vec{A}\cdot\vec{B}=A_1B_1+A_2B_2+A_3B_3=0 \)
then the vectors A and B are perpendicular to each other - [Advanced] Dot product is used to calculate the Work done by a force on any object in a specific direction.
Work done, \( W=Fd\cos\theta \)
Where W is work done by the force F in moving any object through a displacement d when the force makes an angle θ with the displacement vector.
Cross product (Vector product)
Cross product (also called the vector product) is represented by the cross symbol between the two vectors.
Cross product of two vectors \(\vec A\) and \(\vec B\) is defined as
\[ \vec{A}\times\vec{B}=AB\sin\theta\ \ \hat{n} \] (Equation 3)
Result of cross product of vector A and B is also vector.
- The magnitude of cross product \(\vec A \times \vec B\ \) is \(AB \sin\theta\) and it is equal to the area of the parallelogram formed by vector A and B
- The direction of the cross product \(\vec A \times \vec B\) is parallel to unit vector \(\hat n\) which is perpendicular to both vectors A and B at the same time.
Cross product is a bit more tricky than the dot product. \( \cos\theta \) (in dot product) is replaced by \( \sin\theta \) (in cross product), but the result is also multiplied by a unit vector \(\hat n\), So this means the result of the cross product is a vector of magnitude \( AB\sin\theta \) and direction along \(\hat n\).
And there’s another surprise for you! The direction of the unit vector \(\hat n\) is perpendicular to the direction of both vectors A and B at the same time. So if vector A and B lie on one plane, The unit vector \(\hat n\) would lie on another plane which is perpendicular to the plane containing vectors A and B. This means that the cross product happens in 3 dimensions!
Let’s try to understand it with the help of some diagrams
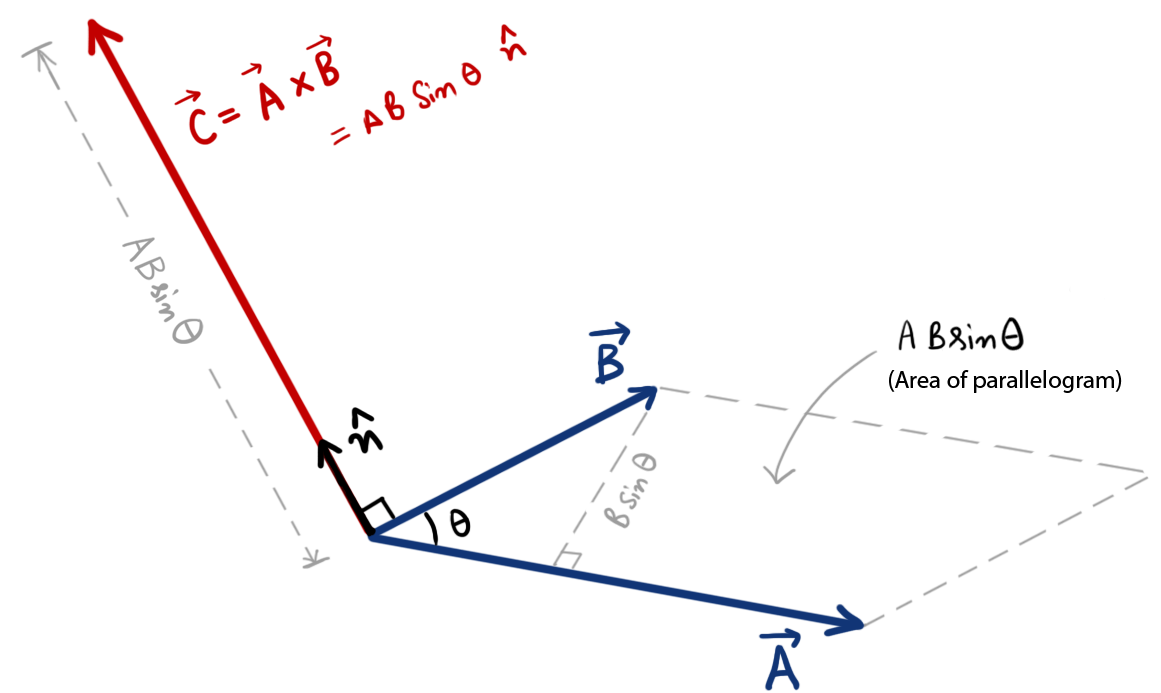
First and foremost, let’s draw \(\vec A\) and \(\vec B\), let’s parallel shift them so that they represent two sides of a parallelogram, while directing away from (or directing towards) each other.
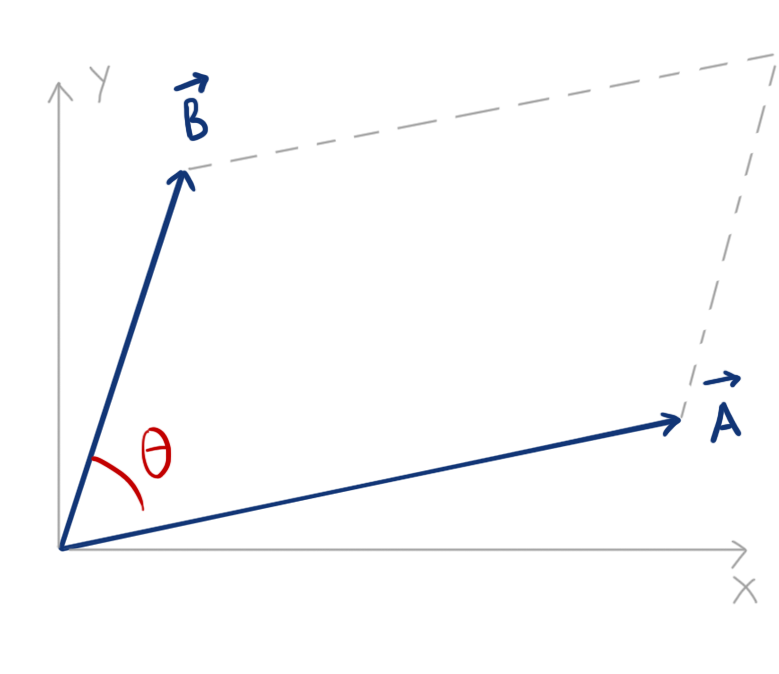
Considering \(\vec A\) as the base, \(B\sin \theta\) will become the height of the parallelogram.
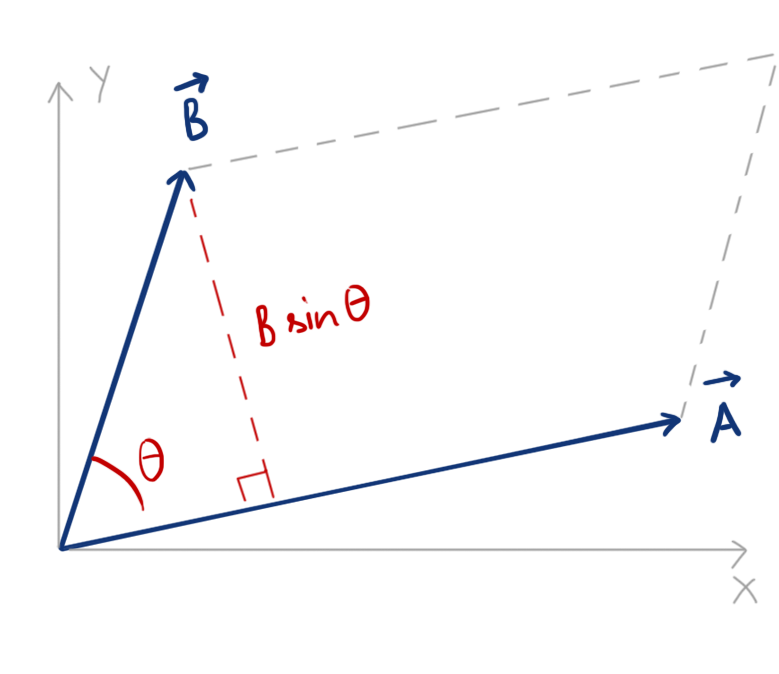
So, the area of the parallelogram formed =
Base of parallelogram \(\times\) Height of parallelogram
\( =\left(A\right)\left(B\sin\theta\right) \)
From Equation 3, It is clear that the magnitude of Cross product of two vectors A and B is equal to the area of the parallelogram formed by the two vectors.
But it also have a direction \(\hat n\) which lies perpendicular to both vector A and B.
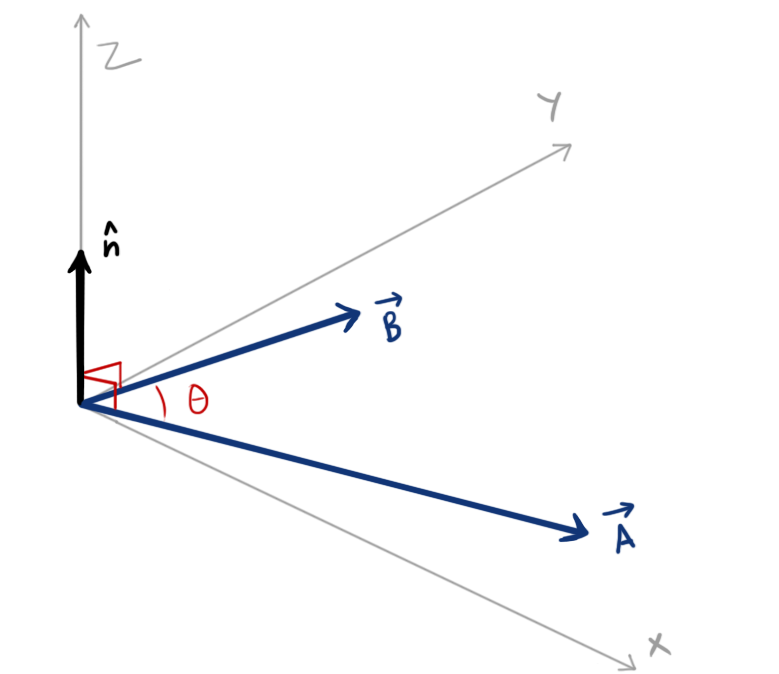
So, If the vectors A and B lie on XY plane of a 3D system XYZ, Then the direction of unit vector \(\hat n\) can be represented along the Z axis which is perpendicular to both vectors A and B as shown in figure.
Note: Vector A and B could lie on any plane, it could be the XY plane (as in this case), YZ plane, XZ plane or even the combination of these three. Then the unit vector \(\hat n\) will change it’s direction accordingly.
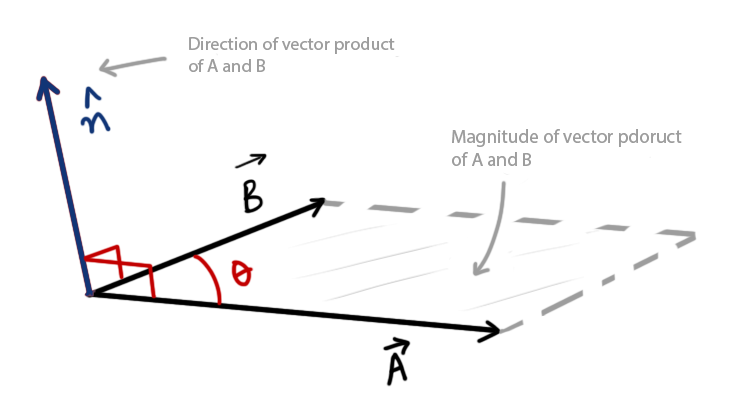
Hence, if \( \vec{C}=\vec{A}\times\vec{B} \), Then the magnitude and direction of \(\vec C\) can be represented with the help of the following diagram
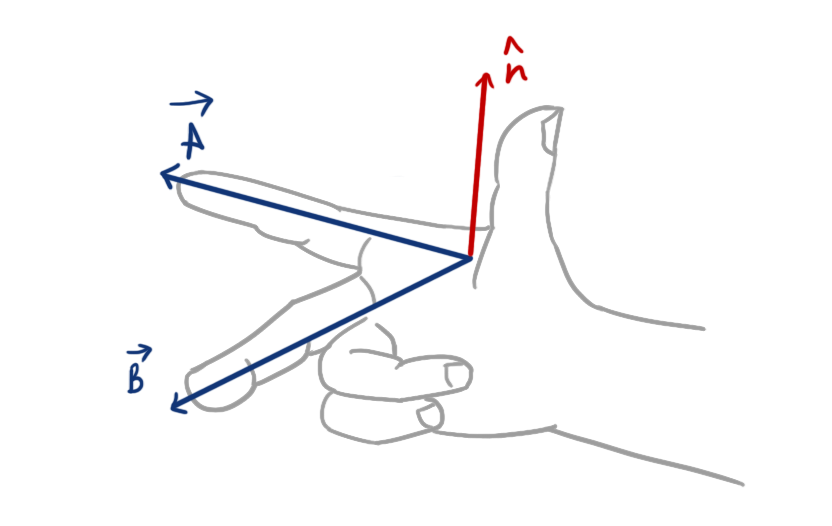
- The direction of unit vector \(\hat n\) is determined by the right hand rule. (whether it is on one side or the other side of the plane containing the vectors A and B)
Algebraic definition of Cross product
Algebraically, If
\( \vec{A}=A_1i+A_2j+A_3k \)
\( \vec{B}=B_1i+B_2j+B_3k \)
then,
\[ \begin{aligned} \vec{A}\times\vec{B}\ =\ \ \ \ &\left(A_2B_3-B_2A_3\right)i\ +\\ &\left(A_3B_1-B_3A_1\right)j\ +\\ &\left(A_1B_2-B_1A_2\right)k \end{aligned} \] \(\Rightarrow\) \[ \vec{A}\times\vec{B}=\left| \begin{matrix} i & j & k\\ A_1 & A_2 & A_3\\ B_1 & B_2 & B_3 \end{matrix} \right| \] (Equation 4)
Following are some important points to remember about cross product:
- Cross product is distributive over addition and subtraction
\( \vec{A}\times\left(\vec{B}+\vec{C}\right)=\vec{A}\times\vec{B}+\vec{A}\times\vec{C} \) - Cross product is NOT commutative
\( \vec{A}\times\vec{B}\ne\vec{B}\times\vec{A} \)
Cross product is anti-commutative
\( \vec{A}\times\vec{B}=-\left(\vec{B}\times\vec{A}\right) \) - Cross product is NOT associative
\( \vec{A}\times\left(\vec{B}\times\vec{C}\right)\ne\left(\vec{A}\times\vec{B}\right)\times\vec{C} \) - Cross product of “two vectors which are parallel to each other” gives a zero vector
If \( \vec{A}\parallel\vec{B} \) then the angle between them is either \(0^{\circ}\) or \( 180^{\circ} \)
\[ \begin{aligned}\Rightarrow\vec{A}\times\vec{B}\ &=AB\sin\theta\ \hat{n}=AB\sin0^{\circ}\ \hat{n}\\&=\vec{0}\end{aligned} \]
Similarly, Cross product of a vector with itself is also zero
\( \vec{A}\times\vec{A}=\vec{0} \) - Cross product of two unit vectors which are perpendicular to each other gives another unit vector which is perpendicular to both. The direction of unit vector is determined by right hand rule.
if, \( \hat{a}\perp\hat{b} \) and \(\hat{c} = \hat{a}\times\hat{b}\)
then, \(\hat{a}\perp\hat{b}\perp\hat{c}\)
Similarly, for a 3D system XYZ, If \(i\ j\) and \(k\) are unit vectors along X, Y, and Z then \(-i\ -j\ -k\) will be the unit vectors along -X, -Y and -Z as shown in the figure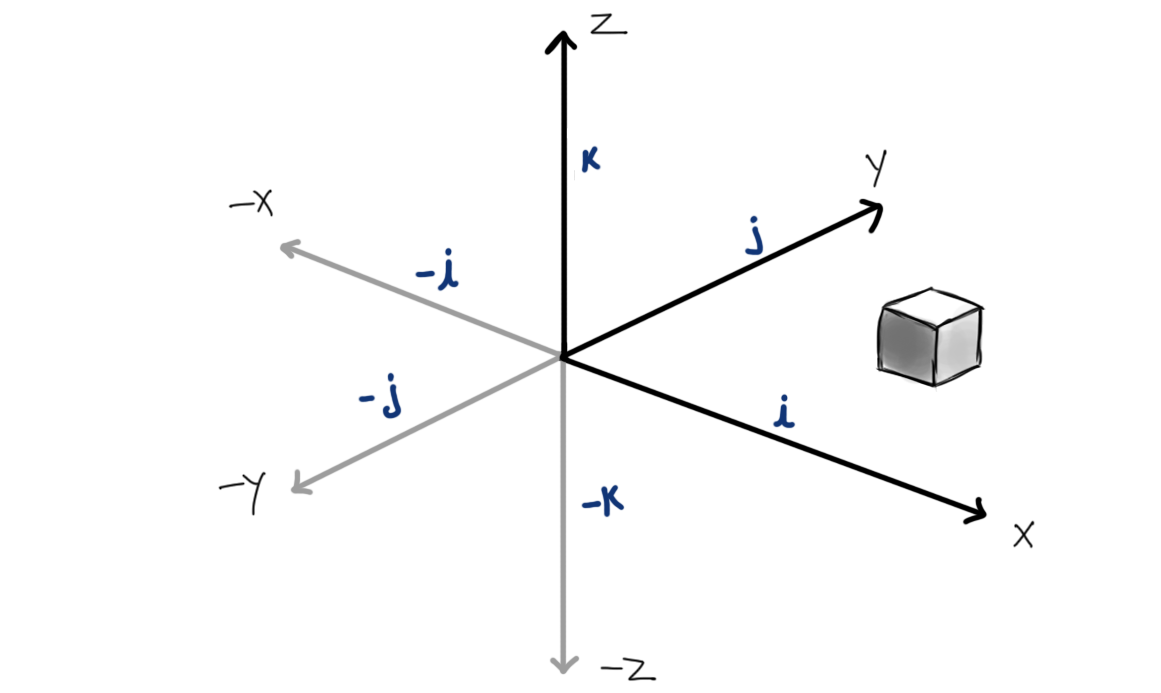
then, \[ \begin{aligned} i\times j=k\\j\times k=i\\ k\times i=j\end{aligned} \] and \[\begin{aligned} j\times i=-k\\ k\times j=-i\\ i\times k=-j \end{aligned}\]
With the help of these equations, since the cross product is also distributive, We can easily derive Equation 4
Some application of Cross product
- Cross product can be used to find a vector which is perpendicular to two known vectors at the same time
- [Advanced] Cross product is used to find the Moment of a force (Torque)
if F is force, d is magnitude of displacement vector, and \(\theta\) is angle between force and displacement vector, then
\( M=Fd\sin\theta\ \hat{n} \)
Position vector
When the job of a vector is to tell the position of a point in 2D or 3D space, Then the vector is known as a position vector.
For example, If a point P has coordinates (x,y) then the point P can be located on the graph with the help of its position vector \(\vec p\), which is given as:
\( \vec{p}=xi+yj \)

Conclusion
Congrats! We finally made it all the way through the tutorial! Here’s a quick summary of what we learned today:
- Any quantity which has magnitude, as well as direction, is a vector.
- Any vector which has a magnitude equal to 1, is called a unit vector.
- vectors can be broken up into its component vectors.
- vectors can be combined (added) to create a resultant vector.
- Two vectors can be multiplied in two ways: (1) Dot product (also called Scalar product) and (2). Cross product (also called Vector product).
- Position vectors are used to tell the position of a point.
Problems
Question 1: If \( \vec{A}=5\vec{B} \), what is the magnitude and direction of \(\vec A\)?
Magnitude of \(\vec A\) is 5 times the magnitude of vector \(\vec B\), magnintude of \(\vec B\) is unknown.
Direction of \(\vec A\) is parallel to the direction of vector \(\vec B\)
Question 2: If \( \vec{A}=5\hat{a} \), What is the magnitude and direction of \(\vec A\)?
Magnitude of \(\vec A\) = 5 * magnitude of unit vector \(\hat a\) = 5 * 1 = 5
Direction of \(\vec A\) is parallel to the unit vector \(\hat a\), Direction of unit vector \(\hat a\) is unknown
Question 3: What is a unit vector?
Unit vectors are just like normal vectors, but with magnitude equal to 1. They are generally denoted by simple letters with a hat symbol above (example \( \hat a \)
Unit vectors having direction parallel to X, Y, and Z axes are usually denoted by \( \hat{i},\hat{j}\text{ and }\hat{k} \) and sometimes just by simple letters \( i,j,\text{ and }k \)
Question 4: If \(\vec A = 5i\), What is the direction and magnitude of \(\vec A\)?
If \(i\) is a unit vector parallel to X axis, then
Magnitude of vector A = 5
Direction of vector A is parallel to unit vector i which is parallel to X axis
Since, 5 is a positive number (greater than 0), Direction of vector A is from left to right(along the positive X axis)
Question 5: What are the components and component vectors of \(\vec A\) along X and Y axis if \( \vec{A}=7i+5j \)?
Component of \(\vec A\)
along X axis = 7
along Y axis = 5
Component vectors of \(\vec A\)
along X axis = \(7i\)
along Y axis = \(5j\)
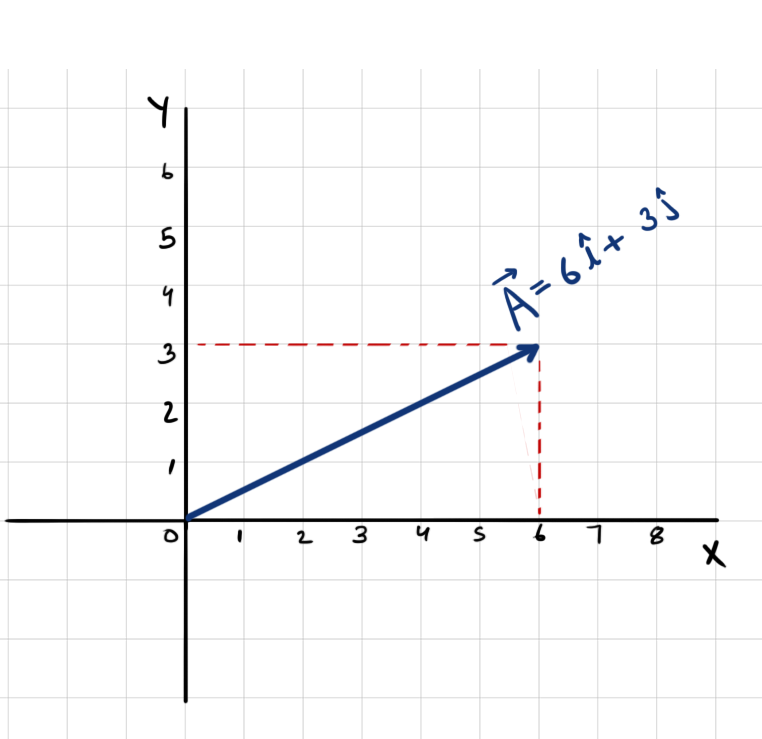
Question 6: If \(\hat{i}\) is a unit vector having direction along positive X axis, and \(\hat{j}\) is unit vector along positive Y axis, Then represent the vector \(\vec{A} = 6\hat{i} + 3\hat{j}\) on an XY graph.
Question 7: What is the magnitude of \(\vec A\) if \( \vec{A}=7i+5j \)?
Magnitude of \( \vec{A}=\ \ A\text{ or }\left|\vec{A}\right|\ \ =\sqrt{7^2+5^2} \)
Question 8: Find a unit vector \(\hat a\) whose direction is parallel to the vector \( \vec{A}=4i-3j \)
magnitude of vector \( \vec{A}=\sqrt{4^2+\left(-3\right)^2}=5 \)
\(\Rightarrow\) vector A can be written as, \( \vec{A}=5\hat{a} \)
where \(\hat{a}\) is a unit vector having direction parallel to that of vector A
Hence,
\[ \begin{aligned} \hat{a}\ &=\frac{\vec{A}}{|\vec{A}|}=\frac{\vec{A}}{5}=\frac{1}{5}\vec{A}\\ \\ &=\frac{4}{5}i-\frac{3}{5}j \end{aligned} \]
Question 9: If \(\vec{A} = -3i\) and \(\vec{B} = 4j\), what is the resultant of these vectors? also tell the magnitude of the resultant.
Resultant of \(\vec{A}\) and \(\vec{B}\) = \(\vec{A} + \vec{B}\)
If \(\vec{R}\) is the resultant, then
\[\begin{aligned}\vec{R}\ &= \vec{A} + \vec{B}\\&=-3i+4j\end{aligned}\]
and magnitude of \(\vec{R}\) = \(R =\sqrt{\left(-3\right)^2+4^2} \)
Question 10: If \( \vec{A}=8i+3j\text{ and }\vec{B}=3i-7j \), find \(\vec{A} + \vec{B}\). Also find its magnitude.
\( \vec{A}+\vec{B}=\left(8+3\right)i+\left(3-7\right)j=11i-4j \)
magnitude = \( \sqrt{11^2+4^2} \)
Question 11: If \( \vec{A}=3i+13j \), Find the angle that \(\vec{A}\) makes with the positive X axis. [Hint]
Angle \[ \theta=\tan^{-1}\left[\frac{13}{3}\right]=77^{\circ} \]
Question 12: If \(\vec{A}\) has magnitude 14, and the angle made by \(\vec{A}\) with positive X axis is \(30^{\circ}\), represent \(\vec{A}\) in terms of it’s component vectors (along X and Y axis). [Hint: This or This]
X component of \[ \vec{A}=A\cos\theta=14\cos30^{\circ}=12.1 \]
Y component of \[ \vec{A}=A\sin\theta=14\sin30^{\circ}=7 \]
\( \Rightarrow\vec{A}=12.1i+7j \)
Question 13: Find the angle between two vectors \( \vec{A}=15i-3j \) and \( \vec{B}=i+4j \). [Hint]
\( A=\sqrt{15^2+3^2}=15.2 \)
\( B=\sqrt{1+4^2}=4.1 \)
\( \vec{A}\cdot\vec{B}=AB\cos\theta=\left(15.2\times4.1\right)\cos\theta=62.3\cos\theta \)
also,
\( \vec{A}\cdot\vec{B}=15\times1+\left(-3\right)\times4=3 \)
with the help of above two equations,
\( 62.3\cos\theta=3 \)
\[ \Rightarrow\theta=\cos^{-1}\left[\frac{3}{62.3}\right]=87.2^{\circ} \]
Question 14: Are the following two vectors parallel to each other? [Hint]
\( \vec{A}=6i+3j \)
\( \vec{B}=-2i-j \)
\[ \vec{A}\times\vec{B}= \left| \begin{matrix} i &j &k\\ 6&3&0\\ -2&-1&0 \end{matrix} \right| = 0 \]
Hence, \(\vec{A} \text{ and } \vec{B}\) are parallel to each other.
Next Part
This page is split into multiple parts.
- Vectors (Physics) | Part-1
- Vectors (Physics) | Part-2
